题目内容
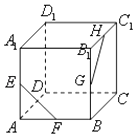
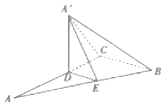
【题目】如图，将直角△ABC沿着平行BC边的直线DE折起，使得平面A′DE⊥平面BCDE，其中D、E分别在AC、AB边上，且AC⊥BC，BC=3，AB=5，点A′为点A折后对应的点，当四棱锥A′-BCDE的体积取得最大值时，求AD的长．
【答案】
【解析】试题分析：由勾股定理易得AC=4，设AD=x，则CD=4﹣x．由△AED∽△ABC，得
，求出四棱锥A′﹣BCDE的体积V（x）=
（0＜x＜4），由此利用导数性质能求出结果．
试题解析：
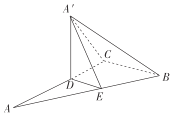
由勾股定理得AC=4，设AD=x，则CD=4-x．
因为△AED∽△ABC，所以
，
则四棱锥A′-BCDE的体积为： 
，
所以
，
当
时，V′（x）＞0，V（x）递增；
当
时，V′（x）＜0，V（x）递减．
故
，
故
时，V（x）取得最大值．
【题目】由于研究性学习的需要，中学生李华持续收集了手机“微信运动”团队中特定20名成员每天行走的步数，其中某一天的数据记录如下：
5860 6520 7326 6798 7325
8430 8215 7453 7446 6754
7638 6834 6460 6830 9860
8753 9450 9860 7290 7850
对这20个数据按组距1000进行分组，并统计整理，绘制了如下尚不完整的统计图表：
步数分组统计表（设步数为x）
组别 | 步数分组 | 频数 |
A | 5500≤x＜6500 | 2 |
B | 6500≤x＜7500 | 10 |
C | 7500≤x＜8500 | m |
D | 8500≤x＜9500 | 2 |
E | 9500≤x＜10500 | n |
（Ⅰ）写出m，n的值，若该“微信运动”团队共有120人，请估计该团队中一天行走步数不少于7500步的人数；
（Ⅱ）记C组步数数据的平均数与方差分别为v1， 
，E组步数数据的平均数与方差分别为v2， 
，试分别比较v1与v2， 
与
的大小；（只需写出结论）
（Ⅲ）从上述A，E两个组别的步数数据中任取2个数据，求这2个数据步数差的绝对值大于3000步的概率．
