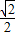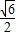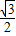题目内容
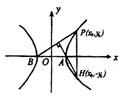 已知双曲线的焦点在x轴上,且过点A(1,0)和B(-1,0),P是双曲线上异于A、B的任一点,如果△APB的垂心H总在双曲线上,求双曲线的标准方程.
已知双曲线的焦点在x轴上,且过点A(1,0)和B(-1,0),P是双曲线上异于A、B的任一点,如果△APB的垂心H总在双曲线上,求双曲线的标准方程.
分析:首先由题意设出双曲线的标准方程,再由A、B两点的坐标可得a=1,然后根据△APB的垂心H总在双曲线上,则由双曲线的对称性可得点P、H关于x轴对称,那么直线PB与直线HA必然互相垂直,因此设出点P的坐标(m,n),进而列出方程组,最后消去参数m、n可解得b,则双曲线方程解决.
解答:解:依题意设双曲线的标准方程为
-
=1,
因为a=1,所以双曲线的标准方程为x2-
=1.
又△APB的垂心H总在双曲线上,所以点P、H关于x轴对称,
设点P的坐标为(m,n),则点H的坐标为(m,-n),
所以
,解得b=1,
故双曲线的标准方程为x2-y2=1.
| x2 |
| a2 |
| y2 |
| b2 |
因为a=1,所以双曲线的标准方程为x2-
| y2 |
| b2 |
又△APB的垂心H总在双曲线上,所以点P、H关于x轴对称,
设点P的坐标为(m,n),则点H的坐标为(m,-n),
所以
|
故双曲线的标准方程为x2-y2=1.
点评:本题考查双曲线的标准方程与性质,同时考查三角形垂心的概念、直线垂直的性质及解方程组的能力.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目
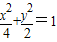 的右焦点作x轴的垂线交椭圆于A、B两点,已知双曲线的焦点在x轴上,对称中心在坐标原点且两条渐近线分别过A、B两点,则双曲线的离心率是( )
的右焦点作x轴的垂线交椭圆于A、B两点,已知双曲线的焦点在x轴上,对称中心在坐标原点且两条渐近线分别过A、B两点,则双曲线的离心率是( )