题目内容
16.已知函数y=f(x)(x∈R)上任一点(x0,f(x0))处的切线斜率k=(x0-3)(x0+1)2,则该函数的单调递减区间为( )| A. | [-1,+∞) | B. | (-∞,3] | C. | (-∞,-1] | D. | [3,+∞) |
分析 由切线的斜率小于等于0,解不等式即可得到所求减区间.
解答 解:任一点(x0,f(x0))处的切线斜率k=(x0-3)(x0+1)2,
由k≤0,解得x0≤3,
即有单调减区间为(-∞,3].
故选B.
点评 本题考查导数的运用:求切线的斜率和单调区间,考查运算能力,属于基础题.

练习册系列答案
相关题目
11.为了了解某地初三年级男生的身高情况,从其中的一个学校选取容量为60的样本(60名男生的身高单位:cm),分组情况如下:
(1)求出表中a,m的值;
(2)画出频率分布直方图;
(3)估计这组数据的众数、平均数和中位数.
| 分组 | 147.5~155.5 | 155.5~163.5 | 163.5~171.5 | 171.5~179.5 |
| 频数 | 6 | 21 | m | |
| 频率 | a | 0.1 |
(2)画出频率分布直方图;
(3)估计这组数据的众数、平均数和中位数.
8.正项数列{an},a1=1,前n项和Sn满足Sn$\sqrt{{S}_{n-1}}$-Sn-1$\sqrt{{S}_{n}}$=2$\sqrt{{S}_{n}{S}_{n-1}}$(n≥2),则a10=( )
| A. | 72 | B. | 80 | C. | 90 | D. | 82 |
6.下列四个集合中,是空集的是( )
| A. | {0} | B. | {x|x>8,且x<5} | C. | {x∈N|x2-1=0} | D. | {x|x>4} |
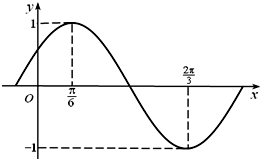 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)部分图象如图所示.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)部分图象如图所示.