题目内容
11.为了了解某地初三年级男生的身高情况,从其中的一个学校选取容量为60的样本(60名男生的身高单位:cm),分组情况如下:| 分组 | 147.5~155.5 | 155.5~163.5 | 163.5~171.5 | 171.5~179.5 |
| 频数 | 6 | 21 | m | |
| 频率 | a | 0.1 |
(2)画出频率分布直方图;
(3)估计这组数据的众数、平均数和中位数.
分析 (1)根据表中数据,求出a、m的值;
(2)补充完整表格,根据表中数据,画出频率分布直方图;
(3)根据频率分布直方图,求出这组数据的众数、平均数与中位数.
解答 解:(1)根据表中数据,得;
∴a=1-0.1-$\frac{6}{60}$-$\frac{21}{60}$=0.45,
m=60×0.1=6;
(2)补充完整表格,如下
| 分组 | 147.5~155.5 | 155.5~163.5 | 163.5~171.5 | 171.5~179.5 |
| 频数 | 6 | 21 | 27 | 6 |
| 频率 | 0.1 | 0.35 | 0.45 | 0.1 |
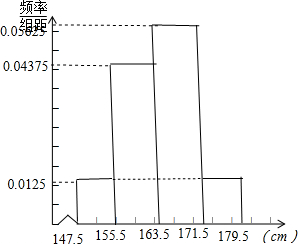
(3)根据频率分布直方图,得;
小矩形图中最高的一组是163.5~171.5,
所以这组数据的众数是$\frac{163.5+171.5}{2}$=167.5,
平均数是
151.5×0.1+159.5×0.35+167.5×0.45+175.5×0.1=163.9;
又∵0.1+0.35=0.45<0.5,
0.45+0.45=0.9>0.5,
∴中位数在163.5~171.5,可设为x,则
(x-163.5)×0.45+0.45=0.5,
解得x=163.6,
∴中位数约为163.6.
点评 本题考查了频率分布直方图的应用问题,也考查了利用分布直方图求众数、平均数与中位数的应用问题,是基础题目.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
2.△ABC中,若sin(A-B)cosB+cos(A-B)sinB≥1,则△ABC是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 不能确定 |
19.为了解某班学生喜爱打篮球是否与性别有关,对该班50名学生进行了问卷调查,得到如图的2×2列联表.
则至少有( )的把握认为喜爱打篮球与性别有关.附参考公式:X2=$\frac{n({n}_{11}{n}_{22}-{n}_{12}{n}_{21})^{2}}{{n}_{1•}{n}_{2•}{n}_{•1}{n}_{•2}}$
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
| P(X2>k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 3.004 | 6.615 | 7.789 | 10.828 |
| A. | 95% | B. | 99% | C. | 99.5% | D. | 99.9% |
16.已知函数y=f(x)(x∈R)上任一点(x0,f(x0))处的切线斜率k=(x0-3)(x0+1)2,则该函数的单调递减区间为( )
| A. | [-1,+∞) | B. | (-∞,3] | C. | (-∞,-1] | D. | [3,+∞) |