Question

设x，y满足约束条件

x-3y+1≥0 2x-3y-1≤0 x≥0，y≥0

，若目标函数z=ax+by（a＞0，b＞0）的最大值为1，则正数a，b满足的关系是

2a+b=1

，

1

a

+

2

b

的最小值是

8

．

Answer 1

分析：先由约束条件画出可行域，如图所示，找出最优解B（2，1），进而使用基本不等式的性质即可求出最小值．

解答：解：由x，y满足约束条件

x-3y+1≥0 2x-3y-1≤0 x≥0，y≥0

，画出可行域如图所示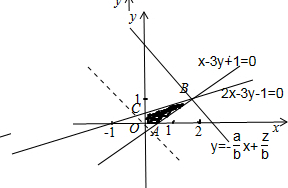：联立

x-3y+1=0 x-3y-1=0

解得

x=2 y=1

，即B（2，1）．
∵a＞0，b＞0，∴-

a

b

＜0，∴当目标函数y=-

a

b

x+

z

b

经过点B（2，1）时，

z

b

取得最大值，即z取得最大值1，
∴2a+b=1．
∴

1

a

+

2

b

=(2a+b)(

1

a

+

2

b

)=2+2+

b

a

+

4a

b

≥4+2

b a × 4a b

=8，当且仅当2a=b=

1

2

时取等号．
故答案为2a+b=1，8．

点评：由约束条件画出可行域并找出最优解及灵活使用基本不等式的性质是解题的关键．