Question

【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且满足.

(1)求角B的大小;

(2)若点M为BC中点,且AM=AC=2,求a的值.

Answer 1

【答案】（1）.（2）.

【解析】试题分析：（1）先利用正弦定理将条件中边角关系转化为角的关系： 再利用两角和正弦公式、诱导公式、三角形内角关系，配角公式化为,最后根据特殊角的三角函数值及三角形内角范围确定角B的大小;（2）利用AM=AC构造直角三角形：取CM中点D, 则△ADB为直角三角形，解出.最后根据余弦定理,得.

试题解析：(1)

即.

∴,∴,所以,得.

(2)取CM中点D,连AD,则AD⊥CM,设,则.

由(1)知,在直角△ADB中, ,∴.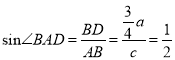

在△ABC中,由余弦定理: ,

即,得.