题目内容
f(x)是定义在D上的函数,若对任何实数α∈(0,1)以及D中的任意两数x1,x2,恒有f(αx1+(1-α)x2)≤αf(x1)+(1-α)f(x2),则称f(x)为定义在D上的C函数.(Ⅰ)试判断函数f1(x)=x2,
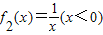 中哪些是各自定义域上的C函数,并说明理由;
中哪些是各自定义域上的C函数,并说明理由;(Ⅱ)已知f(x)是R上的C函数,m是给定的正整数,设an=f(n),n=0,1,2,…,m,且a=0,am=2m,记Sf=a1+a2+…+am.对于满足条件的任意函数f(x),试求Sf的最大值;
(Ⅲ)若(Ⅱ)中Sf的最大值记为h(m),且h(1)+h(2)+…+h(m)≤a对任意给定的正整数m恒成立,试求a的取值范围.
【答案】分析:(Ⅰ)f1(x)=x2是C函数,直接找f(αx1+(1-α)x2)-αf(x1)-(1-α)f(x2),推出其小于等于0即可;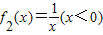 不是C函数,采用举反例的方法即可,x1=-3,x2=-1,
不是C函数,采用举反例的方法即可,x1=-3,x2=-1, .
.
(Ⅱ)先根据定义求出an=f(n)的范围,再结合定义即可求出Sf的最大值;
(Ⅲ)结合(Ⅱ)中Sf的最大值为m2+m,可得h(m)随着自变量的增大,函数值也在增大,所以h(m)没有最大值,其和也没有最大值;即可说明所求的a不存在.
解答:解:(Ⅰ)f1(x)=x2是C函数,证明如下:
对任意实数x1,x2及α∈(0,1),
有f(αx1+(1-α)x2)-αf(x1)-(1-α)f(x2)=(αx1+(1-α)x2)2-αx12-(1-α)x22=-α(1-α)x12-α(1-α)x22+2α(1-α)x1x2=-α(1-α)(x1-x2)2≤0.
即f(αx1+(1-α)x2)≤αf(x1)+(1-α)f(x2).
∴f1(x)=x2是C函数.
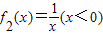 不是C函数,证明如下:
不是C函数,证明如下:
取x1=-3,x2=-1, ,
,
则f(αx1+(1-α)x2)-αf(x1)-(1-α)f(x2)=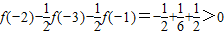 .
.
即f(αx1+(1-α)x2)>αf(x1)+(1-α)f(x2).
∴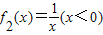 不是C函数.
不是C函数.
(Ⅱ) 对任意0≤n≤m,取x1=m,x2=0, .
.
∵f(x)是R上的C函数,an=f(n),且a=0,am=2m
∴an=f(n)=f(αx1+(1-α)x2)≤αf(x1)+(1-α)f(x2)=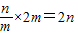 .
.
那么Sf=a1+a2+…+am≤2×(1+2+…+m)=m2+m.
可证f(x)=2x是C函数,且使得an=2n(n=0,1,2,…,m)都成立,此时Sf=m2+m.
综上所述,Sf的最大值为m2+m.
(Ⅲ)∵h(1)+h(2)+…+h(m)≤a对任意给定的正整数m恒成立
所以只需要a大于等于其最大值即可.
因为h(m)=m2+m,当m是正整数时,函数值随自变量的增大而增大;
所以h(m)没有最大值.
故h(1)+h(2)+…+h(m)也没有最大值.
所以所求a不存在.
点评:本题主要是在新定义下考查恒成立问题.恒成立问题一般有两种情况,一是f(x)>a恒成立,只须比f(x)的最小值小即可,二是f(x)<a恒成立,只须比f(x)的最大值大即可.
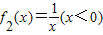 不是C函数,采用举反例的方法即可,x1=-3,x2=-1,
不是C函数,采用举反例的方法即可,x1=-3,x2=-1, .
.(Ⅱ)先根据定义求出an=f(n)的范围,再结合定义即可求出Sf的最大值;
(Ⅲ)结合(Ⅱ)中Sf的最大值为m2+m,可得h(m)随着自变量的增大,函数值也在增大,所以h(m)没有最大值,其和也没有最大值;即可说明所求的a不存在.
解答:解:(Ⅰ)f1(x)=x2是C函数,证明如下:
对任意实数x1,x2及α∈(0,1),
有f(αx1+(1-α)x2)-αf(x1)-(1-α)f(x2)=(αx1+(1-α)x2)2-αx12-(1-α)x22=-α(1-α)x12-α(1-α)x22+2α(1-α)x1x2=-α(1-α)(x1-x2)2≤0.
即f(αx1+(1-α)x2)≤αf(x1)+(1-α)f(x2).
∴f1(x)=x2是C函数.
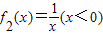 不是C函数,证明如下:
不是C函数,证明如下:取x1=-3,x2=-1,
 ,
,则f(αx1+(1-α)x2)-αf(x1)-(1-α)f(x2)=
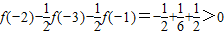 .
.即f(αx1+(1-α)x2)>αf(x1)+(1-α)f(x2).
∴
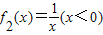 不是C函数.
不是C函数.(Ⅱ) 对任意0≤n≤m,取x1=m,x2=0,
 .
.∵f(x)是R上的C函数,an=f(n),且a=0,am=2m
∴an=f(n)=f(αx1+(1-α)x2)≤αf(x1)+(1-α)f(x2)=
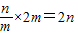 .
.那么Sf=a1+a2+…+am≤2×(1+2+…+m)=m2+m.
可证f(x)=2x是C函数,且使得an=2n(n=0,1,2,…,m)都成立,此时Sf=m2+m.
综上所述,Sf的最大值为m2+m.
(Ⅲ)∵h(1)+h(2)+…+h(m)≤a对任意给定的正整数m恒成立
所以只需要a大于等于其最大值即可.
因为h(m)=m2+m,当m是正整数时,函数值随自变量的增大而增大;
所以h(m)没有最大值.
故h(1)+h(2)+…+h(m)也没有最大值.
所以所求a不存在.
点评:本题主要是在新定义下考查恒成立问题.恒成立问题一般有两种情况,一是f(x)>a恒成立,只须比f(x)的最小值小即可,二是f(x)<a恒成立,只须比f(x)的最大值大即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目