题目内容
f(x)＝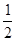
x2＋
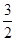x，数列{an}的前n项和为Sn，点(n，Sn)(n∈N*)均在函数y＝f(x)的图象上．
(Ⅰ)求数列{an}的通项公式an；
(Ⅱ)令bn＝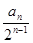
，求数列{bn}的前n项和Tn
【答案】
(Ⅰ)∵点(n，Sn)在f(x)的图象上，
∴Sn＝n2＋n.
当n≥2时，an＝Sn－Sn－1＝n＋1；当n＝1时，a1＝S1＝2，满足上式，∴an＝n＋1(n∈N*)．
(Ⅱ)bn＝＝，
Tn＝b1＋b2＋…＋bn＝2＋＋＋…＋，①
Tn＝＋＋…＋＋，②
由①－②，得Tn＝2＋＋＋…＋－＝(1＋＋＋…＋)＋(1－)＝＋1－＝2(1－)＋1－，
∴Tn＝6－.
【解析】略
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
，x∈(0，＋∞)
x2－2x，g(x)＝logax．如果函数h(x)＝f(x)＋g(x)没有极值点，且
(x)存在零点．
＝2
＋2
，函数g(x)＝x2－x－6．当满足不等式f(x)＞g(x)时，求函数y＝
的最小值．