题目内容
已知函数![]() 在区间[0,1]单调递增,在区间[1,2)单调递减.
在区间[0,1]单调递增,在区间[1,2)单调递减.
(1)求a的值;
(2)若点![]() 在函数f(x)的图象上,求证点A关于直线x=1的对称点B也在函数f(x)的图象上;
在函数f(x)的图象上,求证点A关于直线x=1的对称点B也在函数f(x)的图象上;
(3)是否存在实数b,使得函数g(x)=bx2-1的图象与函数f(x)的图象恰有3个交点,若存在,请求出实数b的值;若不存在,试说明理由.
答案:
解析:
提示:
解析:
|
解:(1)由函数 (2)点A(x0,f(x0))关于直线x=1的对称点B的坐标为(2-x0,f(x0)), ∴点A关于直线x=1的对称点B也在函数f(x)的图象上. (3)函数 |
提示:
|
以导数为载体,考查函数图象的对称性,及方程思想. |

练习册系列答案
相关题目
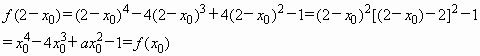
 (3)是否存在实数b,使函数
(3)是否存在实数b,使函数 在区间(0,1)内连续,且
在区间(0,1)内连续,且 .
.

 在区间[0,1]上有最小值-2,求
在区间[0,1]上有最小值-2,求 的值.
的值. 在区间[0,1]上的最大值是2,求实数a的值.
在区间[0,1]上的最大值是2,求实数a的值. 在区间(0,1)内连续,且
在区间(0,1)内连续,且 .
.
