题目内容
如图所示,已知椭圆方程为 ,A为椭圆的左顶点,B、C在椭圆上,若四边形OABC为平行四边形,且
,A为椭圆的左顶点,B、C在椭圆上,若四边形OABC为平行四边形,且 ,则椭圆的离心率等于( )
,则椭圆的离心率等于( )
A、 B、
B、 C、
C、 D、
D、
C
解析试题分析:令椭圆的右端点为M,连接CM,由题意四边形OABC为平行四边形,且∠OAB=45°,B,C在椭圆上,可得∠COM=∠CMO=∠OAB=45°,则有∠OCM=90°,故可得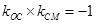 ,又四边形OABC为平行四边形,B,C在椭圆上,由图形知|BC|=a,且BC∥OA由椭圆的对称性知,B,C两点关于y轴对称,故C的横坐标为
,又四边形OABC为平行四边形,B,C在椭圆上,由图形知|BC|=a,且BC∥OA由椭圆的对称性知,B,C两点关于y轴对称,故C的横坐标为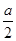 ,代入椭圆的方程得
,代入椭圆的方程得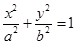 得y=±
得y=±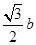 ,由图形知C(
,由图形知C(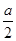 ,
,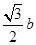 ),故有
),故有 ,∴
,∴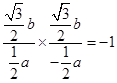 ,解得
,解得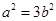 ,故
,故 ,所以
,所以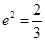
,得e=
考点:本题考查椭圆的简单性质。
点评:求解本题的关键是根据椭圆的对称性得出点C的坐标以及图形中的垂直关系,求出点C的坐标是为了表示出斜率,求出垂直关系是为了利用斜率的乘积为-1建立方程,然后再根据求离心率的公式求出离心率即可.本题比较抽象,方法单一,入手较难,运算量不大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设 是椭圆
是椭圆 上的一点,
上的一点, 为焦点,且
为焦点,且 ,则
,则 的面积为( )
的面积为( )
A. | B. | C. | D.16 |
椭圆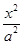 +
+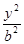 =1(a>b>0)的离心率是
=1(a>b>0)的离心率是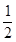 ,则
,则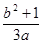 的最小值为( )
的最小值为( )
A.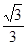 | B.1 | C.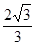 | D.2 |
双曲线方程为 ,则它的右焦点坐标为 ( )。
,则它的右焦点坐标为 ( )。
A. | B. | C.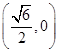 | D. |
已知 ,
,  是椭圆的两个焦点,若满足
是椭圆的两个焦点,若满足 的点M总在椭圆的内部,则椭圆离心率的取值范围是( )
的点M总在椭圆的内部,则椭圆离心率的取值范围是( )
| A.(0, 1) | B. | C. | D. |
已知抛物线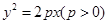 的焦点为
的焦点为 ,点
,点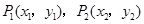 ,
,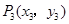 在抛物线上,且
在抛物线上,且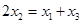 , 则有 ( )
, 则有 ( )
A. | B.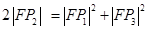 |
C. | D.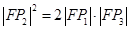 |
双曲线 的离心率为
的离心率为 ,则它的渐近线方程为
,则它的渐近线方程为
A. | B. | C. | D. |
 的左焦点
的左焦点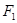 作斜率为1的直线,该直线与双曲线的两条渐近线的交点分别为A、B,若
作斜率为1的直线,该直线与双曲线的两条渐近线的交点分别为A、B,若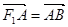 ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( )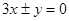 B.
B.
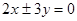 D.
D.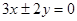
 的焦点
的焦点 的直线与抛物线交于A、B两点,抛物线准线与x轴交于C点,若
的直线与抛物线交于A、B两点,抛物线准线与x轴交于C点,若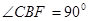 ,则|AF|-|BF|的值为( )
,则|AF|-|BF|的值为( )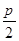 B.
B.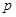 C.
C.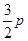 D.
D.