Question

已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0．|φ|＜

π

2

）在一个周期内的部分函数图象如图所示．
（Ⅰ）求函数f（x）的解析式．
（Ⅱ）求函数f（x）的单调递增区间．
（Ⅲ）求函数f（x）在区间[0，1]上的最大值和最小值．

Answer 1

分析：（I）由已知中函数f（x）=Asin（ωx+φ）（A＞0，ω＞0．|φ|＜

π

2

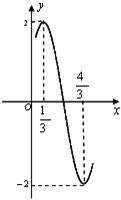
）在一个周期内的部分函数图象，我们易求出函数的最大值，最小值，周期等信息，结合A，ω，φ与函数最值、周期之间的关系，易求出函数的解析式．
（II）根据（I）中所求的函数的解析式，结合正弦型函数单调性的确定方法，即可求出函数f（x）=Asin（ωx+φ）（A＞0，ω＞0．|φ|＜

π

2

）的单调递增区间．
（Ⅲ）根据（II）的结论，我们易分析出函数在区间[0，1]上的单调性，进而得到函数f（x）在区间[0，1]上的最大值和最小值．

解答：解：（Ⅰ）由图可得当X=

1

3

时，函数有最大值2；当X=

4

3

时，函数有最小值-2；
∴A=2，
T=2=

2π

ω

，即ω=π
∴f（x）=2sin（πx+φ）
又∵函数图象过（

1

3

，2）点，|φ|＜

π

2

∴2=2sin（

1

3

π+φ），
解得φ=

π

6

∴f（x）=2sin（πx+

π

6

）
（II）令2kπ-

π

2

≤πx+

π

6

≤2kπ+

π

2

，k∈Z
则2k-

2

3

≤x≤2k+

1

3

，k∈Z
∴函数f（x）=2sin（πx+

π

6

）的单调递增区间为[2k-

2

3

，2k+

1

3

]，（k∈Z）
（III）由（II）的结论我们可得，
函数f（x）=2sin（πx+

π

6

）在区间[0，

1

3

]上单调递增，在区间[

1

3

，1]上单调递减，
∴当X=

1

3

时，函数f（x）=2sin（πx+

π

6

）取最大值2，当X=1时，函数f（x）=2sin（πx+

π

6

）取最小值-1．

点评：本题考查的知识点是由函数f（x）=Asin（ωx+φ）的部分图象确定其解析式，正弦函数的单调性，三角函数的最值，其中根据函数的部分图象确定函数的解析式是解答本题的关键．