题目内容
已知函数f（x）=x2-2ax+3，命题P：f（x）在区间[2，3]上的最小值为f（2）；命题Q：方程f（x）=0的两根x1，x2满足x1＜-1＜x2．若命题P与命题Q中有且只有一个真命题，求实数a的取值范围．
【答案】分析：结合二次函数的性质可得，f（x）=（x-a）2+3-a2，对于命题 P：由f（x）在区间[2，3]上的最小值为f（2）可求a的范围；对于命题Q：方程f（x）=0的两根x1，x2满足x1＜-1＜x2，则可得f（-1）＜0，可求a的范围，若P或Q中只有一个为真可知有两种情况：①P真，Q假，②P假，Q真，分别可求a的范围
解答：解：f（x）=（x-a）2+3-a2，对称轴x=a，
对于命题 P：∵f（x）在区间[2，3]上的最小值为f（2），∴a≤2；
对于命题Q：方程f（x）=0的两根x1，x2满足x1＜-1＜x2，∴f（-1）＜0，∴a＜-2
∴当P真，Q假时，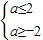
∴-2≤a≤2
当P假，Q真时，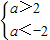
∴a∈Φ
综上，a的取值范围是[-2，2]．
点评：本题主要考查了命题真假的应用，解题的关键是熟练利用二次函数的性质及一元二次方程的实根分布求解参数的取值范围．
解答：解：f（x）=（x-a）2+3-a2，对称轴x=a，
对于命题 P：∵f（x）在区间[2，3]上的最小值为f（2），∴a≤2；
对于命题Q：方程f（x）=0的两根x1，x2满足x1＜-1＜x2，∴f（-1）＜0，∴a＜-2
∴当P真，Q假时，
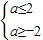∴-2≤a≤2当P假，Q真时，
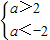∴a∈Φ综上，a的取值范围是[-2，2]．
点评：本题主要考查了命题真假的应用，解题的关键是熟练利用二次函数的性质及一元二次方程的实根分布求解参数的取值范围．
练习册系列答案
文敬图书课时先锋系列答案
相关题目
已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|