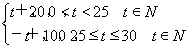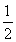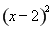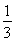题目内容
若实数a、b、c、d满足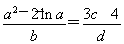
＝1，则(a－c)2＋(b－d)2的最小值为________．
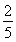(1－ln2)2
【解析】∵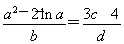
＝1，∴b＝a2－2lna，d＝3c－4，∴点(a，b)在曲线y＝x2－2lnx上，点(c，d)在曲线y＝3x－4上，(a－c)2＋(b－d)2的几何意义就是曲线y＝x2－2lnx到曲线y＝3x－4上点的距离最小值的平方．考查曲线y＝x2－2lnx(x>0)平行于直线y＝3x－4的切线，∵y′＝2x－
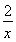，令y′＝2x－
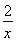＝3，解得x＝2，∴切点为(2，4－2ln2)，该切点到直线y＝3x－4的距离d＝
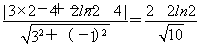就是所要求的两曲线间的最小距离，故(a－c)2＋(b－d)2的最小值为d2＝
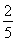(1－ln2)2.
练习册系列答案
相关题目
若函数f(x)＝x3＋x2－2x－2的一个正数零点附近的函数值用二分法计算，其参考数据如下：
f(1)＝－2 | f(1.5)＝0.625 | f(1.25)＝－0.984 |
f(1.375)＝－0.260 | f(1.4375)＝0.162 | f(1.40625)＝－0.054 |
那么方程x3＋x2－2x－2＝0的一个近似根为________(精确到0.1)．
