题目内容

已知A+B= $数学公式$ ，则（1+tanA）（1+tanB）=

A.
$数学公式$
B.
1
C.
$数学公式$
D.
2

D
分析：由题意，可将（1+tanA）（1+tanB）展开为1+tanA+tanB+tanAtanB，再结合两角和的正切公式及A+B= $\text{[math]}$ 即可求出值，选出正确答案
解答：∵A+B= $\text{[math]}$
∴（1+tanA）（1+tanB）
=1+tanA+tanB+tanAtanB
=1+tan（A+B）（1-tanAtanB）+tanAtanB
=1+tan $\text{[math]}$ （1-tanAtanB）+tanAtanB
=1+1=2
故选D
点评：本题考点是两角和与差的正切函数，考查了正切的和角公式及其变形，解题的关键是理解正切的和角公式，能对其灵活运用求值，熟练掌握公式可以使得变形时更灵活

练习册系列答案

同步拓展阅读系列答案

同步作文与创新阅读系列答案

1号卷期末整理与复习系列答案

金牌学案风向标系列答案

中考新视野系列答案

同步作文新讲练系列答案

高中学业水平考试复习学与练指导精编丛书系列答案

高效复习计划小学毕业升学总复习系列答案

优加学案口算题卡系列答案

全真模拟试卷精编系列答案

相关题目

=（2，-1，0），

=（0，3，-2），则cos＜

＞的值为（　　）

设复数z₁=1+2ai，z₂=a-i（a∈R），A={z||z-z1|＜

}，B={z||z-z2|≤2

}，已知A∩B=∅，则a的取值范围是

已知a∈R，则“

≤0”是“指数函数y=a^x在R上为减函数”的（　　）

A、充分不必要条件

B、必要不充分条件

C、充要条件

D、既不充分也不必要条件

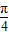，则（1+tanA）（1+tanB）=（）
A．