题目内容
已知椭圆方程
+
=1(1＜a≤5)，过其右焦点做斜率不为0的直线l与椭圆交于A，B两点，设在A，B两点处的切线交于点M（x0，y0），则M点的横坐标x0的取值范围是（ ）
| x2 |
| a2 |
| y2 |
| 2a-1 |
分析：依题意，a2-（2a-1）=（a-1）2＞0，椭圆
+
=1（1＜a≤5）的焦点在x轴，作图可知，当过右焦点的直线l垂直于x轴时，M点的横坐标x0最小，求得此时的椭圆的切线方程，即可求得M点的横坐标x（即x0），从而可求其值（即最小值），当l绕右焦点F顺时针旋转时，x0的取值越来越大，直至无穷．
| x2 |
| a2 |
| y2 |
| 2a-1 |
解答：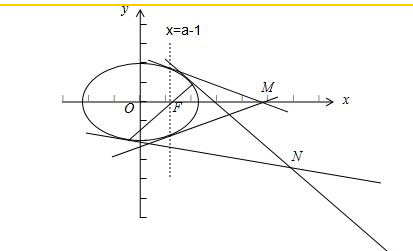
解：依题意，a2-（2a-1）=（a-1）2＞0，
∴方程为
+
=1（1＜a≤5）的椭圆的焦点在x轴，
作图如右：
由图知，当l过其右焦点且垂直于x轴时，M点的横坐标x0最小，
∵F（a-1，0），
∴AB⊥x轴时，l的方程为x=a-1，
由
得：A（a-1，
），B（a-1，-
）（1＜a≤5），
∵过A（a-1，
）点的椭圆的切线方程为：
x+
y=1，
∴令y=0，得x=
=
=（a-1）+
+2，
∵1＜a≤5，
∴x=（a-1）+
+2≥4（当且仅当a=2时取“=”）．
∴x≥4．
当l绕右焦点F顺时针旋转时，x0的取值越来越大，直至无穷．
∴M点的横坐标x0的取值范围是[4，+∞）．
故选：A．
解：依题意，a2-（2a-1）=（a-1）2＞0，∴方程为
| x2 |
| a2 |
| y2 |
| 2a-1 |
作图如右：
由图知，当l过其右焦点且垂直于x轴时，M点的横坐标x0最小，
∵F（a-1，0），
∴AB⊥x轴时，l的方程为x=a-1，
由
|
| 2a-1 |
| a |
| 2a-1 |
| a |
∵过A（a-1，
| 2a-1 |
| a |
| a-1 |
| a2 |
| ||
| b2 |
∴令y=0，得x=
| a2 |
| a-1 |
| [(a-1)+1]2 |
| a-1 |
| 1 |
| a-1 |
∵1＜a≤5，
∴x=（a-1）+
| 1 |
| a-1 |
∴x≥4．
当l绕右焦点F顺时针旋转时，x0的取值越来越大，直至无穷．
∴M点的横坐标x0的取值范围是[4，+∞）．
故选：A．
点评：本题考查椭圆的性质，着重考查椭圆与直线方程的综合应用，属于难题．
练习册系列答案
寒假学与练系列答案
相关题目