题目内容
(本小题满分12分)
函数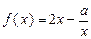 的定义域为
的定义域为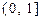 (
(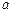 为实数).
为实数).
(1)当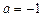 时,求函数
时,求函数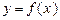 的值域;
的值域;
(2)若函数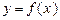 在定义域上是减函数,求
在定义域上是减函数,求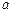 的取值范围;
的取值范围;
(3)函数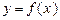 在
在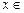
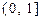 上的最大值及最小值,并求出函数取最值时
上的最大值及最小值,并求出函数取最值时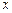 的值
的值
函数
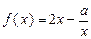 的定义域为
的定义域为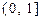 (
(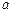 为实数).
为实数).(1)当
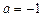 时,求函数
时,求函数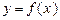 的值域;
的值域;(2)若函数
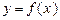 在定义域上是减函数,求
在定义域上是减函数,求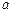 的取值范围;
的取值范围;(3)函数
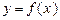 在
在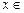
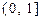 上的最大值及最小值,并求出函数取最值时
上的最大值及最小值,并求出函数取最值时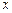 的值
的值(1)函数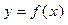 的值域为
的值域为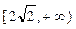
(2)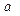 的取值范围是
的取值范围是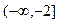
(3)当 时,函数
时,函数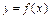 在
在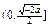 上单调减,在
上单调减,在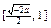 上单调增,无最大值,
上单调增,无最大值,
当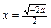 时取得最小值
时取得最小值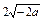
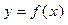 的值域为
的值域为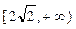
(2)
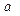 的取值范围是
的取值范围是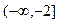
(3)当
 时,函数
时,函数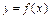 在
在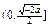 上单调减,在
上单调减,在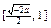 上单调增,无最大值,
上单调增,无最大值,当
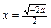 时取得最小值
时取得最小值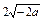
解:(1)显然函数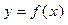 的值域为
的值域为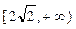 ; ……………3分
; ……………3分
(2)若函数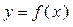 在定义域上是减函数,则任取
在定义域上是减函数,则任取
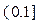 且
且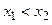 都有
都有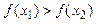 成立, 即
成立, 即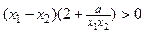
只要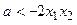 即可,
即可,
由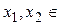
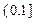 ,故
,故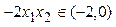 ,所以
,所以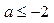 ,
,
故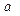 的取值范围是
的取值范围是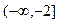 ;
;
(3)当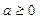 时,函数
时,函数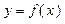 在
在 上单调增,无最小值,
上单调增,无最小值,
当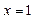 时取得最大值
时取得最大值 ;
;
由(2)得当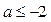 时,函数
时,函数 在
在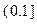 上单调减,无最大值,
上单调减,无最大值,
当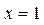 时取得最小值
时取得最小值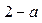 ;
;
当 时,函数
时,函数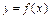 在
在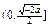 上单调减,在
上单调减,在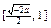 上单调增,无最大值,
上单调增,无最大值,
当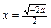 时取得最小值
时取得最小值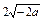 .
.
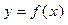 的值域为
的值域为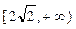 ; ……………3分
; ……………3分(2)若函数
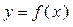 在定义域上是减函数,则任取
在定义域上是减函数,则任取
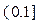 且
且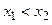 都有
都有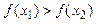 成立, 即
成立, 即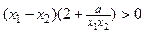
只要
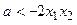 即可,
即可, 由
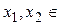
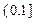 ,故
,故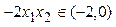 ,所以
,所以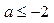 ,
,故
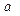 的取值范围是
的取值范围是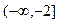 ;
; (3)当
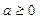 时,函数
时,函数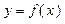 在
在 上单调增,无最小值,
上单调增,无最小值,当
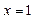 时取得最大值
时取得最大值 ;
;由(2)得当
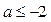 时,函数
时,函数 在
在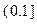 上单调减,无最大值,
上单调减,无最大值,当
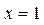 时取得最小值
时取得最小值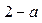 ;
;当
 时,函数
时,函数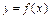 在
在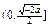 上单调减,在
上单调减,在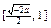 上单调增,无最大值,
上单调增,无最大值,当
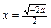 时取得最小值
时取得最小值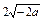 .
. 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
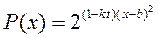 (其中t为关税的税率,且
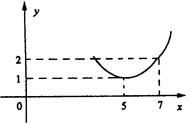
(其中t为关税的税率,且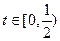 ).(x为市场价格,b、k为正常数),当t=
).(x为市场价格,b、k为正常数),当t=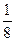 时的市场供应量曲线如图 (1)根据图象求k、b的值;
时的市场供应量曲线如图 (1)根据图象求k、b的值;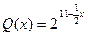 .
.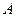 产品,拟开发新产品
产品,拟开发新产品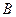 ,根据市场调查与预测,
,根据市场调查与预测,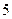 万元,其利润与投资额关系为
万元,其利润与投资额关系为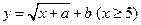 ,如图二.(单位:万元)
,如图二.(单位:万元) 两种产品的利润
两种产品的利润 表示为投资金额
表示为投资金额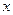 的函数关系式;
的函数关系式;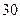 万元资金
万元资金 ,并全部投入两种产品的生产,问:怎样分配这
,并全部投入两种产品的生产,问:怎样分配这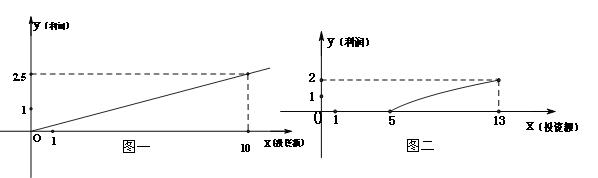
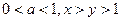 ,则下列关系式中正确的个数是 ( )
,则下列关系式中正确的个数是 ( )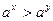 ②
②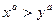
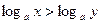 ④
④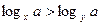
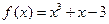 的零点最接近的是 ( )
的零点最接近的是 ( )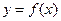 的图象按向量
的图象按向量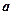 平移后,得到函数
平移后,得到函数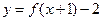 的图象,则向量
的图象,则向量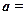 ( )
( )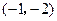
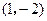
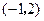
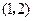
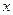 的方程
的方程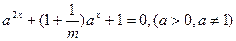 有解,则实数
有解,则实数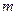 的取值范围是
的取值范围是
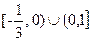
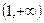
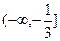
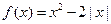 ,方程
,方程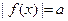 有6个不同的实根.则实数
有6个不同的实根.则实数 的取值范围是 ( )
的取值范围是 ( )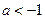
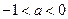
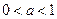
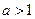
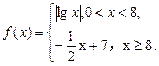 ,若
,若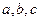 互不相等,且
互不相等,且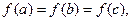 则
则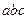 的取值范围是 .
的取值范围是 .