题目内容
有下列命题:
①设集合M={x|0<x≤3},N={x|0<x≤2},则“a∈M”是“a∈N”的充分而不必要条件;
②命题:“若a∈M,则b M”的逆否命题是:若b∈M,则a
M”的逆否命题是:若b∈M,则a M;
M;
③若p∧q是假命题,则p、q都是假命题;
④命题P:“ x0∈R,x
x0∈R,x -x0-1>0”的否定
-x0-1>0”的否定 P:“
P:“ x∈R,x2-x-1≤0”.
x∈R,x2-x-1≤0”.
其中真命题的序号是________.
【答案】
②④
【解析】
试题分析:本题考查的知识点是,判断命题真假.(1)考查了集合间的关系,在集合M中任取一个x值,看其是否在集合N中,反之,在集合N中任取一个x值,判断其是否又在集合M中;(2)考查命题的逆否命题,把原命题的结论取否定作为条件,条件取否定作为结论;(3)考查复合命题的真假判断,两个命题中只要有一个假命题,则p∧q为假命题;(4)考查特称命题的否定,注意特称命题的否定全称命题的格式.解:对于①,a在集合M中取值为3,但3不在集合N中,有a∈M,但a?N,所以“a∈M”是“a∈N”的不充分条件,所以①不正确;对于②,把原命题的结论取否定作为条件,条件取否定作为结论,所以,命题“若a∈M,则b?M”的逆否命题是:若b∈M,则a?M,所以命题②正确;
对于③,假若p,q中有一个为真命题,则p∧q也是假命题,所以,命题③不正确;对于④,特称命题的否定是全称命题,所以命题P:“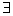 x0∈R,x
x0∈R,x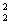 -x0-1>0”的否定¬P:“?x∈R,x2-x-1≤0”正确正确,故②④
-x0-1>0”的否定¬P:“?x∈R,x2-x-1≤0”正确正确,故②④
考点:命题的真假判断
点评:本题考查了命题的真假判断与运用,解答的关键是熟练基本概念,掌握有关格式,如特称命题否定的格式 特称命题P:?x0∈M,p(x0),否定¬p:?x∈M,¬p(x).

练习册系列答案
相关题目
 的解集是
的解集是 .
.