题目内容
(本小题满分12分)
已知椭圆 的焦点在
的焦点在 轴上,离心率为
轴上,离心率为 ,对称轴为坐标轴,且经过点
,对称轴为坐标轴,且经过点 .
.
(I)求椭圆 的方程;
的方程;
(II)直线 与椭圆
与椭圆 相交于
相交于 、
、 两点,
两点,  为原点,在
为原点,在 、
、 上分别存在异于
上分别存在异于 点的点
点的点 、
、 ,使得
,使得 在以
在以 为直径的圆外,求直线斜率
为直径的圆外,求直线斜率 的取值范围.
的取值范围.
【答案】
(I)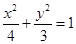 ;(II)
;(II)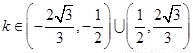 。
。
【解析】
试题分析:(I)依题意,可设椭圆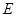 的方程为
的方程为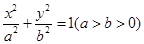 .
.
由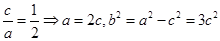
∵ 椭圆经过点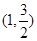 ,则
,则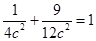 ,解得
,解得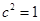
∴ 椭圆的方程为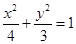 …………………
…………………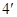
(II)联立方程组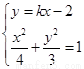 ,消去
,消去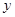 整理得
整理得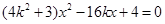 ………………
………………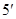
∵ 直线与椭圆有两个交点,
∴ 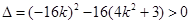 ,解得
,解得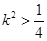 ①…………………
①…………………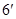
∵ 原点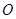 在以
在以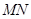 为直径的圆外,
为直径的圆外,
∴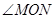 为锐角,即
为锐角,即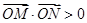 .
.
而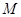 、
、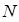 分别在
分别在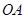 、
、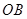 上且异于
上且异于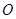 点,即
点,即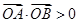 ………………
………………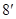
设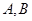 两点坐标分别为
两点坐标分别为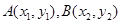 ,
,
则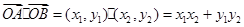
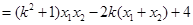
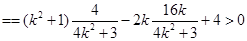
解得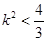 ,
②…………………
,
②…………………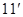
综合①②可知: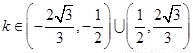 …………………
…………………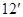
考点:椭圆的标准方程;椭圆的简单性质;直线与椭圆的综合应用。
点评:(1)有关直线与椭圆的综合应用,经常用到的步骤为:设点→联立方程→消元→韦达定理。(2)在第二问中,合理转化是解题的关键,即把“O在以MN为直径的圆外”这个条件转化为“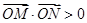 ”。
”。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目