题目内容
在直四棱柱ABCD-A1B1C1D1中,DB=BC,DB⊥AC,点M是棱BB1上一点.
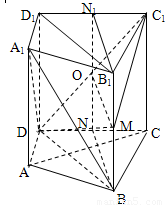
(1)求证:B1D1∥平面A1BD;
(2)求证:MD⊥AC;
(3)试确定点M的位置,使得平面DMC1⊥平面CC1D1D.
(1)见解析. (2)见解析.(3)当点M为棱BB1的中点时,平面DMC1⊥平面CC1D1D.
【解析】
试题分析:(1)由直四棱柱概念,得BB1//DD1,
得到四边形BB1D1D是平行四边形,从而B1D1∥BD,由直线与平面平行的判定定理即得证.
(2)注意到BB1⊥平面ABCD,AC⊂平面ABCD,推出BB1⊥AC.
又BD⊥AC,即得AC⊥平面BB1D1D.而MD⊂平面BB1D1D,故得证.
(3)分析预见当点M为棱BB1的中点时,符合题意.此时取DC的中点N,D1C1的中点N1,连接NN1交DC1于O,连接OM,证得BN⊥DC.又DC是平面ABCD与平面DCC1D1的交线,而平面ABCD⊥平面DCC1D1,推出BN⊥平面DCC1D1.又可证得,O是NN1的中点,由四边形BMON是平行四边形,得出OM⊥平面CC1D1D,得证.
试题解析:(1)由直四棱柱概念,得BB1//DD1,
∴四边形BB1D1D是平行四边形,∴B1D1∥BD.
而BD⊂平面A1BD,B1D1⊄平面A1BD,∴B1D1∥平面A1BD.
(2)∵BB1⊥平面ABCD,AC⊂平面ABCD,∴BB1⊥AC.
又∵BD⊥AC,且BD∩BB1=B,∴AC⊥平面BB1D1D.
而MD⊂平面BB1D1D,∴MD⊥AC.
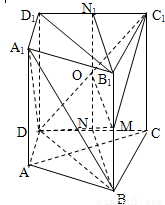
(3)当点M为棱BB1的中点时,取DC的中点N,D1C1的中点N1,连接NN1交DC1于O,连接OM,如图所示.
∵N是DC的中点,BD=BC,∴BN⊥DC.又∵DC是平面ABCD与平面DCC1D1的交线,而平面ABCD⊥平面DCC1D1,∴BN⊥平面DCC1D1.
又可证得,O是NN1的中点,∴BM∥ON且BM=ON,即四边形BMON是平行四边形,∴BN∥OM,∴OM⊥平面CC1D1D,因为OM⊂面DMC1,所以平面DMC1⊥平面CC1D1D.
考点:线面平行的判定定理,线面垂直的判定及性质,面面垂直的判定,四棱柱的几何特征.

 华东师大版一课一练系列答案
华东师大版一课一练系列答案 在直四棱柱ABCD-A1B1C1D1中,AA1=2,底面是边长为1的正方形,E、G、F分别是棱B1B、D1D、DA的中点.
在直四棱柱ABCD-A1B1C1D1中,AA1=2,底面是边长为1的正方形,E、G、F分别是棱B1B、D1D、DA的中点. 在直四棱柱ABCD-A1B1C1D1中,已知AB∥CD,AB=AD=1,D1D=CD=2,AB⊥AD.
在直四棱柱ABCD-A1B1C1D1中,已知AB∥CD,AB=AD=1,D1D=CD=2,AB⊥AD.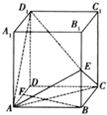 在直四棱柱ABCD-A1B1C1D1中,AA1=2,底面是边长为1的正方形,E、F分别是棱B1B、DA的中点.
在直四棱柱ABCD-A1B1C1D1中,AA1=2,底面是边长为1的正方形,E、F分别是棱B1B、DA的中点. 如图,在直四棱柱ABCD-A1B1C1D1中,点E,F分别在AA1,CC1上,且AE=
如图,在直四棱柱ABCD-A1B1C1D1中,点E,F分别在AA1,CC1上,且AE= 在直四棱柱ABCD-A1B1C1D1中,底面ABCD为直角梯形,∠BAD=∠ADC=90°,AB=AD=1,CD=CC1=2,E为棱AA1的中点,F为棱BB1上的动点.
在直四棱柱ABCD-A1B1C1D1中,底面ABCD为直角梯形,∠BAD=∠ADC=90°,AB=AD=1,CD=CC1=2,E为棱AA1的中点,F为棱BB1上的动点.