题目内容
 在直四棱柱ABCD-A1B1C1D1中,底面ABCD为直角梯形,∠BAD=∠ADC=90°,AB=AD=1,CD=CC1=2,E为棱AA1的中点,F为棱BB1上的动点.
在直四棱柱ABCD-A1B1C1D1中,底面ABCD为直角梯形,∠BAD=∠ADC=90°,AB=AD=1,CD=CC1=2,E为棱AA1的中点,F为棱BB1上的动点.(Ⅰ)试确定点F的位置,使得D1E⊥DF;
(Ⅱ)在(Ⅰ)的条件下,求CF与平面EFD1所成角的大小.
分析:(Ⅰ)F为棱BB1上的中点,通过三垂线定理即可证明D1E⊥DF;
(Ⅱ)在(Ⅰ)的条件下,通过点C到平面EFD1的距离等于点D到平面EFD1的距离的转化,然后求CF与平面EFD1所成角的大小.
(Ⅱ)在(Ⅰ)的条件下,通过点C到平面EFD1的距离等于点D到平面EFD1的距离的转化,然后求CF与平面EFD1所成角的大小.
解答: 解:(Ⅰ)因为E为棱AA1的中点,当F为棱BB1上的中点,
解:(Ⅰ)因为E为棱AA1的中点,当F为棱BB1上的中点,
因为直四棱柱ABCD-A1B1C1D1中,底面ABCD为直角梯形,
∠BAD=∠ADC=90°,所以,点F在平面A1AD内的射影为点E,
直线DE?平面A1AD,
而D1E⊥DE,
由三垂线定理可知,DF⊥D1E,
∴D1E⊥DF;
(Ⅱ)由(Ⅰ)可知,F为棱BB1上的中点,
∴EF∥AB,AB∥CD,
∴CD∥EF,CD?平面EFD1,EF?平面EFD1
∴CD∥平面EFD1,
∴点C到平面EFD1的距离等于点D到平面EFD1的距离,
∵AE=1,AD=1,DE=
,
即点C到平面EFD1的距离为
.
CF=
=
.
∴sinθ=
=
,又θ∈[0 ,
],
∴θ=arcsin
.
CF与平面EFD1所成角的大小为arcsin
.
 解:(Ⅰ)因为E为棱AA1的中点,当F为棱BB1上的中点,
解:(Ⅰ)因为E为棱AA1的中点,当F为棱BB1上的中点,因为直四棱柱ABCD-A1B1C1D1中,底面ABCD为直角梯形,
∠BAD=∠ADC=90°,所以,点F在平面A1AD内的射影为点E,
直线DE?平面A1AD,
而D1E⊥DE,
由三垂线定理可知,DF⊥D1E,
∴D1E⊥DF;
(Ⅱ)由(Ⅰ)可知,F为棱BB1上的中点,
∴EF∥AB,AB∥CD,
∴CD∥EF,CD?平面EFD1,EF?平面EFD1
∴CD∥平面EFD1,
∴点C到平面EFD1的距离等于点D到平面EFD1的距离,
∵AE=1,AD=1,DE=
| 2 |
即点C到平面EFD1的距离为
| 2 |
CF=
| FB2+BC2 |
| 3 |
∴sinθ=
| ||
|
| ||
| 3 |
| π |
| 2 |
∴θ=arcsin
| ||
| 3 |
CF与平面EFD1所成角的大小为arcsin
| ||
| 3 |
点评:本题是中档题,考查直线与直线垂直的证明,直线与平面所成的角的求法,考查空间想象能力,定理的灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
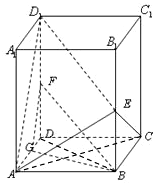 在直四棱柱ABCD-A1B1C1D1中,AA1=2,底面是边长为1的正方形,E、G、F分别是棱B1B、D1D、DA的中点.
在直四棱柱ABCD-A1B1C1D1中,AA1=2,底面是边长为1的正方形,E、G、F分别是棱B1B、D1D、DA的中点.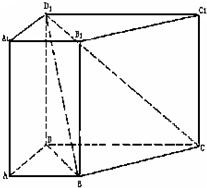 在直四棱柱ABCD-A1B1C1D1中,已知AB∥CD,AB=AD=1,D1D=CD=2,AB⊥AD.
在直四棱柱ABCD-A1B1C1D1中,已知AB∥CD,AB=AD=1,D1D=CD=2,AB⊥AD.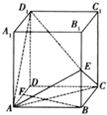 在直四棱柱ABCD-A1B1C1D1中,AA1=2,底面是边长为1的正方形,E、F分别是棱B1B、DA的中点.
在直四棱柱ABCD-A1B1C1D1中,AA1=2,底面是边长为1的正方形,E、F分别是棱B1B、DA的中点. 如图,在直四棱柱ABCD-A1B1C1D1中,点E,F分别在AA1,CC1上,且AE=
如图,在直四棱柱ABCD-A1B1C1D1中,点E,F分别在AA1,CC1上,且AE=