题目内容
函数f（x）=sinx+cosx+1在P（x，y）点处的切线平行于直线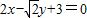
，求y的值．
【答案】分析：由f（x）=sinx+cosx+1在P（x，y）点处的切线平行于直线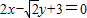
，知
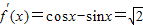，由此知x=2kπ-
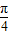，k∈Z，从而能求出y的值．
解答：解：∵f（x）=sinx+cosx+1，
∴f′（x）=cosx-sinx，
∵f（x）=sinx+cosx+1在P（x，y）点处的切线平行于直线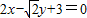
，
∴
，
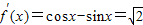∴cos（x+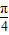
）=1，
∴x=2kπ-
，k∈Z，
即x=2kπ-
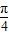，k∈Z，
∴y=sinx+cosx+1=1．
点评：本题考查切线的几何意义的求法，解题时要认真审题，仔细解答，注意三角函数性质的灵活运用．
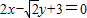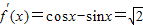，知，由此知x=2kπ-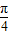，k∈Z，从而能求出y的值．解答：解：∵f（x）=sinx+cosx+1，
∴f′（x）=cosx-sinx，
∵f（x）=sinx+cosx+1在P（x，y）点处的切线平行于直线
，∴
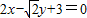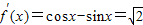，∴cos（x+
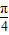）=1，∴x=2kπ-
，k∈Z，即x=2kπ-
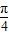，k∈Z，∴y=sinx+cosx+1=1．
点评：本题考查切线的几何意义的求法，解题时要认真审题，仔细解答，注意三角函数性质的灵活运用．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
函数f（x）=sin（ωx+?）（x∈R，ω＞0，0≤?＜2π）的部分图象如图，则