题目内容
9．cos27°cos57°-sin27°cos147°等于（ ）| A． | $\frac{{\sqrt{3}}}{2}$ | B． | -$\frac{{\sqrt{3}}}{2}$ | C． | $\frac{1}{2}$ | D． | -$\frac{1}{2}$ |
分析 利用诱导公式可得cos147°=cos（90°+57°）=sin57°，结合两角差的余弦函数公式即可求值得解．
解答 解：cos27°cos57°-sin27°cos147°
=cos27°cos57°-sin27°cos（90°+57°）
=cos27°cos57°+sin27°sin57°
=cos（57°-27°）
=cos30°
=$\frac{\sqrt{3}}{2}$．
故选：A．
点评 本题主要考查了诱导公式，两角差的余弦函数公式的综合应用，属于基本知识的考查．
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
20．如果女大学生身高x（cm）与体重y（kg）的关系满足线性回归模型y=0.85x-88+e，其中|e|≤4，如果已知某女大学生身高160cm，则体重预计不会低于（ ）
| A． | 44 kg | B． | 46 kg | C． | 50 kg | D． | 54 kg |
17．集合A={x|2x2+4ax+1=0}中只有一个元素，则a的值是（ ）
| A． | $\frac{\sqrt{2}}{2}$ | B． | $\frac{1}{2}$ | C． | ±$\frac{\sqrt{2}}{2}$ | D． | 2或$\frac{\sqrt{2}}{2}$ |
4．正四面体ABCD边长为a，点E、F分别是BC、AD的中点，则$\begin{array}{l}→\\{AE}\end{array}•\begin{array}{l}→\\{AF}\end{array}$的值为（ ）
| A． | a2 | B． | $\frac{1}{2}{a^2}$ | C． | $\frac{1}{4}{a^2}$ | D． | $\frac{{\sqrt{3}}}{4}{a^2}$ |
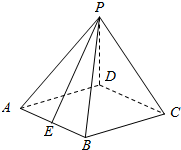如图，在四棱锥P-ABCD中，底面ABCD是菱形，∠DAB=60°，平面PED⊥平面PAB，PD⊥AD，点E为AB中点．