题目内容
定义在R上的函数 ,对任意不等的实数
,对任意不等的实数 都有
都有 成立,又函数
成立,又函数 的图象关于点(1,0)对称,若不等式
的图象关于点(1,0)对称,若不等式 成立,则当1≤x<4时,
成立,则当1≤x<4时, 的取值范围是
的取值范围是
A. | B. | C. | D. |
A
解析试题分析:解:因为对任意不等实数x1,x2满足 所以函数f(x)是定义在R上的单调递减函数.因为函数y=f(x-1)的图象关于点(1,0)对称,所以函数y=f(x)的图象关于点(0,0)对称,即函数f(x)是定义在R上的奇函数.又因为对于任意的x,y∈R,不等式f(x2-2x)+f(2y-y2)≤0成立,所以f(x2-2x)≥f(-2y+y2)成立,所以根据函数的单调性可得:对于任意的x,y∈R,不等式x2-2x≥y2-2y成立,即(x-y)(x+y-2)≥0(1≤x≤4),所以可得其可行域,如图所示:
所以函数f(x)是定义在R上的单调递减函数.因为函数y=f(x-1)的图象关于点(1,0)对称,所以函数y=f(x)的图象关于点(0,0)对称,即函数f(x)是定义在R上的奇函数.又因为对于任意的x,y∈R,不等式f(x2-2x)+f(2y-y2)≤0成立,所以f(x2-2x)≥f(-2y+y2)成立,所以根据函数的单调性可得:对于任意的x,y∈R,不等式x2-2x≥y2-2y成立,即(x-y)(x+y-2)≥0(1≤x≤4),所以可得其可行域,如图所示: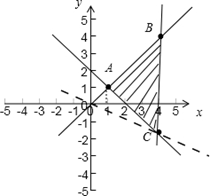
因为 =
= 所以
所以 表示点(x,y)与点(0,0)连线的斜率,所以结合图象可得:
表示点(x,y)与点(0,0)连线的斜率,所以结合图象可得: 的最小值是直线OC的斜率-
的最小值是直线OC的斜率- ,最大值是直线AB的斜率1,所以
,最大值是直线AB的斜率1,所以 的范围为:[
的范围为:[ 故答案为:
故答案为:
考点:抽象函数的性质
点评:解决此类问题的关键是熟练掌握抽象函数的性质的证明与判断,如单调性、奇偶性的证明与判断,并且熟练的利用函数的性质解有关的不等式,以及熟练掌握线性规划问题,此题综合性较强知识点也比较零散,对学生掌握知识与运用知识的能力有一定的要求.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
下列各组函数中表示同一函数的是( )
A. 与 与 |
B. 与 与 |
C. 与 与 |
D. 与 与 |
函数f(x)=x- 的零点是( )
的零点是( )
| A.0 | B.1 | C.2 | D.无数个 |
定义在 上的函数
上的函数 ,满足
,满足 ,
,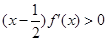 ,若
,若 且
且 ,则有( ).
,则有( ).
A. | B. | C. | D.不能确定 |
若函数 上不是单调函数,则实数k的取值范围是( )
上不是单调函数,则实数k的取值范围是( )
A. | B. |
C. | D.不存在这样的实数k |
国际上钻石的重量计量单位是克拉,已知某种钻石的价值V(美元)与其重量W(克拉)之间的函数关系为 ,若把一颗钻石切割成1︰3的两颗钻石,则价值损失的百分率为( )(价值损失百分率
,若把一颗钻石切割成1︰3的两颗钻石,则价值损失的百分率为( )(价值损失百分率 ,切割中重量损耗不计)
,切割中重量损耗不计)
| A.12.5% | B.37.5% | C.50% | D.62.5% |
 的一个零点所在的区
的一个零点所在的区 ,则
,则 的值为( )
的值为( )


 的图象的顶点在第四象限,则函数
的图象的顶点在第四象限,则函数 的图象是( ).
的图象是( ).

 的图象是连续不断的,且有如下对应值表:
的图象是连续不断的,且有如下对应值表:

