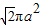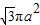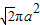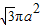题目内容
在侧棱长为3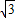
的正三棱锥P-ABC中，∠APB=∠BPC=∠CPA=40°过点A作截面AEF与PB、PC侧棱分别交于E、F两点，则截面的周长最小值为（ ）A．4
B．2
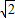
C．10
D．9
【答案】分析：将三棱锥的侧面展开，则截面的周长最小值的最小值，即可转化为求AA1的长度，解三角形PAA1，即可得到答案．
解答：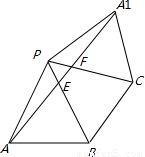
解：将三棱锥的侧面A展开，如图，
则图中∠APA1=120°，
AA1为所求，
由余弦定理可得AA1=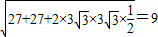
，
故选D．
点评：本题考查的知识点是棱锥的结构特征，其中将三棱锥的侧面展开，将空间问题转化为平面上两点间距离问题，是解答本题的关键．
解答：
解：将三棱锥的侧面A展开，如图，则图中∠APA1=120°，
AA1为所求，
由余弦定理可得AA1=
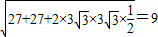，故选D．
点评：本题考查的知识点是棱锥的结构特征，其中将三棱锥的侧面展开，将空间问题转化为平面上两点间距离问题，是解答本题的关键．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
侧棱长为a的正三棱锥P-ABC的侧面都是直角三角形，且四个顶点都在一个球面上，则该球的表面积为（ ）
A、
| ||
| B、2πa2 | ||
C、
| ||
| D、3πa2 |
