题目内容
若不等式x2+2xy≤a(x2+y2)对于一切正数x,y恒成立,则实数a的最小值为
- A.2
- B.
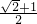
- C.

- D.

D
分析:x2+2xy≤a(x2+y2)?2xy≤(a-1)x2+ay2?(a-1) -2×
-2× +a≥0对于一切正数x,y恒成立,依题意,令f(t)=(a-1)t2-2t+a,列不等式组
+a≥0对于一切正数x,y恒成立,依题意,令f(t)=(a-1)t2-2t+a,列不等式组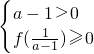 ,解之即可得答案.
,解之即可得答案.
解答:∵x>0,y>0,
∴x2+2xy≤a(x2+y2))?2xy≤(a-1)x2+ay2?(a-1) -2×
-2× +a≥0,
+a≥0,
令t= (t>0),f(t)=(a-1)t2-2t+a,
(t>0),f(t)=(a-1)t2-2t+a,
依题意,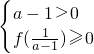 即
即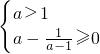 ,解得a≥
,解得a≥ .
.
∴实数a的最小值为 .
.
故选D.
点评:本题考查函数恒成立问题,考查转化与构造函数思想,考查解不等式组的能力,属于难题.
分析:x2+2xy≤a(x2+y2)?2xy≤(a-1)x2+ay2?(a-1)
 -2×
-2× +a≥0对于一切正数x,y恒成立,依题意,令f(t)=(a-1)t2-2t+a,列不等式组
+a≥0对于一切正数x,y恒成立,依题意,令f(t)=(a-1)t2-2t+a,列不等式组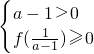 ,解之即可得答案.
,解之即可得答案.解答:∵x>0,y>0,
∴x2+2xy≤a(x2+y2))?2xy≤(a-1)x2+ay2?(a-1)
 -2×
-2× +a≥0,
+a≥0,令t=
 (t>0),f(t)=(a-1)t2-2t+a,
(t>0),f(t)=(a-1)t2-2t+a,依题意,
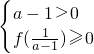 即
即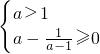 ,解得a≥
,解得a≥ .
.∴实数a的最小值为
 .
.故选D.
点评:本题考查函数恒成立问题,考查转化与构造函数思想,考查解不等式组的能力,属于难题.

练习册系列答案
相关题目

