题目内容
.(本小题满分12分)
水库的蓄水量随时间而变化,现用t表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于t的近似函数关系式为
V(t)=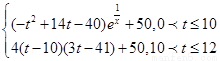 。
。
(Ⅰ)该水库的蓄求量小于50的时期称为枯水期,以i-1<t<t表示第1月份(i=1,2,…,12),同一年内哪几个月份是枯水期?
(Ⅱ)求一年内该水库的最大蓄水量(取e=2.7计算)
【答案】
(Ⅰ)枯水期为1月,2月,3月,4月,11月,12月共6个月。
(Ⅱ)一年内该水库的最大蓄水量是108.32亿立方米。
【解析】(Ⅰ)①当时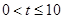 ,
,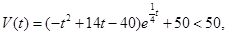
化简得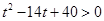 ,
,
解得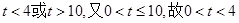 。
。
②当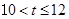 时,
时,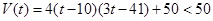 ,
,
化简得,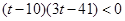
解得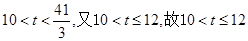 .
.
综上得,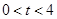 ,或
,或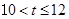 。
。
故知枯水期为1月,2月,3月,4月,11月,12月共6个月。
(Ⅱ)由(Ⅰ)知,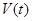 的最大值只能在(4,10)内内达到。
的最大值只能在(4,10)内内达到。
由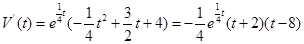 ,
,
令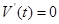 ,解得
,解得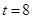 (
(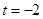 舍去)。
舍去)。
当 变化时,
变化时,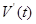 与
与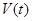 的变化情况如下表:
的变化情况如下表:
|
|
(4,8) |
8 |
(8,10) |
|
|
+ |
0 |
- |
|
|
|
极大值 |
|
由上表,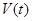 在
在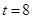 时取得最大值
时取得最大值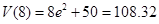 (亿立方米)。
(亿立方米)。
故知一年内该水库的最大蓄水量是108.32亿立方米。
第(Ⅰ)问实际上就是解不等式,当然要注意问题的转化;第(Ⅱ)问求最值要先求导再通过单调性求最值。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
