题目内容
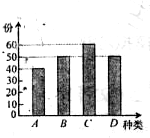 (2012•枣庄一模)学校餐厅新推出A、B、C、D四款套餐,某一天四款套餐销售情况的条形图如图所示.为了了解同学们对新推出的四款套餐的评价,对就餐的每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面的表格所示:
(2012•枣庄一模)学校餐厅新推出A、B、C、D四款套餐,某一天四款套餐销售情况的条形图如图所示.为了了解同学们对新推出的四款套餐的评价,对就餐的每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面的表格所示:| 满意 | 一般 | 不满意 | |
| A套餐 | 50% | 25% | 25% |
| B套餐 | 80% | 0 | 20% |
| C套餐 | 50% | 50% | 0 |
| D套餐 | 40% | 20% | 40% |
(2)若想从调查问卷被选中且填写不满意的同学中选出两人进行面谈,列举基本事件,并求这两人中至少有1人选择是D款套餐的概率.
分析:(1)根据题意,由条形图可得,选择A、B、C、D四款套餐的人数,将其相加可得总人数,结合分层抽样方法,计算可得答案;
(2)由(1)可得,抽取的选择A、B、C、D四款套餐的人数,结合题意可得其中填写不满意的人数依次为1、1、0、2,记选择A套餐填写不满意的为a,选择B套餐填写不满意的为b,选择D套餐填写不满意的为c、d,列举从4人中任选2人的情况,可得其情况数目,分析可得其中至少有1人选择是D款套餐的情况数目,由古典概型公式,计算可得答案.
(2)由(1)可得,抽取的选择A、B、C、D四款套餐的人数,结合题意可得其中填写不满意的人数依次为1、1、0、2,记选择A套餐填写不满意的为a,选择B套餐填写不满意的为b,选择D套餐填写不满意的为c、d,列举从4人中任选2人的情况,可得其情况数目,分析可得其中至少有1人选择是D款套餐的情况数目,由古典概型公式,计算可得答案.
解答:解:(1)由条形图可得,选择A、B、C、D四款套餐的人数依次为40、50、60、50,共有40+50+60+50=200人,
从中用分层抽样的方法从调查问卷中抽取20份,
其中选择A套餐的人数为40×
=4,
选择B套餐的人数为50×
=5,
选择C套餐的人数为60×
=6,
选择A套餐的人数为50×
=5,
则抽取的选择A、B、C、D四款套餐的人数依次为4、5、6、5;
(2)由(1)可得,抽取的选择A、B、C、D四款套餐的人数依次为4、5、6、5,其中填写不满意的人数依次为1、1、0、2,
记选择A套餐填写不满意的为a,选择B套餐填写不满意的为b,选择D套餐填写不满意的为c、d,
从4人中任选2人,有(a、b)、(a,c)、(a,d)、(b,c)、(b,d)、(c,d),共6种情况,
其中至少有1人选择是D款套餐的有5种情况,
则选出2人中至少有1人选择是D款套餐的概率为
.
从中用分层抽样的方法从调查问卷中抽取20份,
其中选择A套餐的人数为40×
| 20 |
| 200 |
选择B套餐的人数为50×
| 20 |
| 200 |
选择C套餐的人数为60×
| 20 |
| 200 |
选择A套餐的人数为50×
| 20 |
| 200 |
则抽取的选择A、B、C、D四款套餐的人数依次为4、5、6、5;
(2)由(1)可得,抽取的选择A、B、C、D四款套餐的人数依次为4、5、6、5,其中填写不满意的人数依次为1、1、0、2,
记选择A套餐填写不满意的为a,选择B套餐填写不满意的为b,选择D套餐填写不满意的为c、d,
从4人中任选2人,有(a、b)、(a,c)、(a,d)、(b,c)、(b,d)、(c,d),共6种情况,
其中至少有1人选择是D款套餐的有5种情况,
则选出2人中至少有1人选择是D款套餐的概率为
| 5 |
| 6 |
点评:本题考查条形图的运用、分层抽样方法以及古典概型的计算,关键是根据条形图,得到相关的数据信息.

练习册系列答案
相关题目
 (2012•枣庄一模)如图,CDEF是以圆O为圆心,半径为1的圆的内接正方形,将一颗豆子随机地扔到该圆内,用A表示事件“豆子落在扇形OCFH内”(点H将劣弧
(2012•枣庄一模)如图,CDEF是以圆O为圆心,半径为1的圆的内接正方形,将一颗豆子随机地扔到该圆内,用A表示事件“豆子落在扇形OCFH内”(点H将劣弧
 (2012•枣庄一模)给定两个长度为1的平面向量
(2012•枣庄一模)给定两个长度为1的平面向量