题目内容

A是由定义在［2,4］上且满足如下条件的函数φ(x)组成的集合:①对任意x∈［1,2］,都有φ(2x)∈(1,2);②存在常数L(0＜L＜1),使得对任意的x1,x2∈［1,2］,都有|φ(2x1)-φ(2x2)|≤L|x1-x2|.

(1)设φ(x)=,x∈［2,4］,证明φ(x)∈A;

(2)设φ(x)∈A,如果存在x0∈(1,2),使得x0=φ(2x0),那么这样的x0是唯一的;

(3)设φ(x)∈A,任取x1∈(1,2),令xn+1=φ(2xn),n=1,2,…,证明给定正整数k,对任意的正整数p,成立不等式|xk+p-xk|≤|x2-x1|.

证明:(1)对任意的x∈［1,2］,φ(2x)=,x∈［1,2］,≤φ(2x)≤,1＜＜＜2,所以φ(2x)∈(1,2).

对任意的x1,x2∈［1,2］,

|φ(2x1)-φ(2x2)|

=|x1-x2|,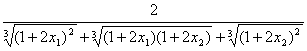

3＜,

所以0＜＜,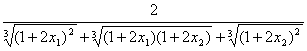

令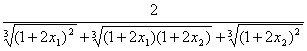=L,0＜L＜1,

|φ(2x1)-φ(2x2)|≤L|x1-x2|.

所以φ(x)∈A.

(2)反证法:假设存在两个x0,x0′∈(1,2),x0≠x0′,使得x0=φ(2x0),x0′=φ(2x0′),则

由|φ(2x0)-φ(2x0′)|≤L|x0-x0′|,得|x0-x0′|≤L|x0-x0′|,所以L≥1,矛盾,故结论成立,

(3)|x3-x2|=|φ(2x2)-φ(2x1)|≤L|x2-x1|,所以|xn+1-xn|≤Ln-1|x2-x1|,

|xk+p-xk|=|(xk+p-xk+p-1)+(xk+p-1-xk+p-2)+…+(xk+1-xk)|≤|xk+p-xk+p-1|+|xk+p-1-xk+p-2|+…+|xk+1-xk|≤Lk+p-2|x2-x1|+Lk+p-3|x2-x1|+…+Lk-1|x2-x1|≤|x2-x1|.

练习册系列答案
相关题目
（2013•延庆县一模）A是由定义在[2，4]上且满足如下条件的函数φ（x）组成的集合：
（1）对任意x∈[1，2]，都有φ（2x）∈（1，2）；
（2）存在常数L（0＜L＜1），使得对任意的x1，x2∈[1，2]，都有|φ（2x1）-φ（2x2）|≤L|x1-x2|．
（Ⅰ）设φ（x）=
31+x
，x∈[1，2]，证明：φ（x）∈A；
（Ⅱ）设φ（x）∈A，如果存在x0∈（1，2），使得x0=φ（2x0），那么这样的x0是唯一的．
（2013•延庆县一模）A是由定义在[2，4]上且满足如下条件的函数φ（x）组成的集合：
（1）对任意x∈[1，2]，都有φ（2x）∈（1，2）；
（2）存在常数L（0＜L＜0），使得对任意的x1，x2∈[1，2]，都有|?（2x1）-?（2x2）|≤L|x1-x2|．
（Ⅰ）设φ（x）=
31+x
，x∈[2，4]，证明：φ（x）∈A；
（Ⅱ）设φ（x）∈A，如果存在x0∈（1，2），使得x0=φ（2x0），那么这样的x0是唯一的；
（Ⅲ）设φ（x）∈A，任取xn∈（1，2），令xn+1=φ（2nx），n=1，2，…，证明：给定正整数k，对任意的正整数p，不等式|xk+p-xk|≤
Lk-1
1-L
|x2-x1|成立．
A是由定义在[2，4]上且满足如下条件的函数φ（x）组成的集合：
（1）对任意x∈[1，2]，都有φ（2x）∈（1，2）；
（2）存在常数L（0＜L＜0），使得对任意的x1，x2∈[1，2]，都有|?（2x1）-?（2x2）|≤L|x1-x2|．
（Ⅰ）设φ（x）=
31+x
，x∈[2，4]，证明：φ（x）∈A；
（Ⅱ）设φ（x）∈A，如果存在x0∈（1，2），使得x0=φ（2x0），那么这样的x0是唯一的；
（Ⅲ）设φ（x）∈A，任取xn∈（1，2），令xn+1=φ（2nx），n=1，2，…，证明：给定正整数k，对任意的正整数p，不等式|xk+p-xk|≤
Lk-1
1-L
|x2-x1|成立．
A是由定义在［2,4］上且满足如下条件的函数φ(x)组成的集合:

①对任意x∈［1,2］,都有φ(2x)∈(1,2);

②存在常数L(0＜L＜1),使得对任意x1、x2∈［1,2］,都有|φ(2x1)-φ(2x2)|≤L|x1-x2|.

(1)设φ(x)=,x∈［2,4］,证明φ(x)∈A;

(2)设φ(x)∈A,证明如果存在x0∈(1,2),使得x0=φ(2x0),那么这样的x0是唯一的;

(3)设φ(x)∈A,任取x1∈(1,2),令xn+1=φ(2xn),n=1,2,…,证明给定正整数k,对任意的正整数p,成立不等式:|xk+p-xk|≤|x1-x2|.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网