题目内容
设P(x,y)是椭圆
思路分析:利用斜率的坐标公式分别求出kPA与kPB的值,利用椭圆的方程找出x与y的关系,代入即可.
解:∵点P的纵坐标y≠0,∴x≠±5.
∴kPA=![]() ,kPB=
,kPB=![]() .
.
∴kPA·kPB=![]() .
.
∵点P在椭圆![]() =1上,
=1上,
∴y2=16×(![]() )=16×
)=16×![]() .
.
把y2=16×![]() 代入kPA·kPB=
代入kPA·kPB=![]() ,得kPA·kPB=
,得kPA·kPB=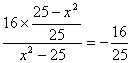 .
.
∴kPA·kPB为定值,这个定值是![]() .
.

练习册系列答案
相关题目
题目内容
设P(x,y)是椭圆
思路分析:利用斜率的坐标公式分别求出kPA与kPB的值,利用椭圆的方程找出x与y的关系,代入即可.
解:∵点P的纵坐标y≠0,∴x≠±5.
∴kPA=![]() ,kPB=
,kPB=![]() .
.
∴kPA·kPB=![]() .
.
∵点P在椭圆![]() =1上,
=1上,
∴y2=16×(![]() )=16×
)=16×![]() .
.
把y2=16×![]() 代入kPA·kPB=
代入kPA·kPB=![]() ,得kPA·kPB=
,得kPA·kPB=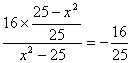 .
.
∴kPA·kPB为定值,这个定值是![]() .
.
