题目内容
已知直线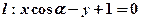 。
。
(Ⅰ)当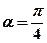 时,求直线
时,求直线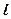 的斜率;
的斜率;
(Ⅱ)若直线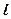
 的倾斜角为
的倾斜角为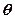 ,求
,求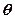 范围。
范围。
解 :(Ⅰ)当
:(Ⅰ)当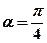 时,
时, ; 3分
; 3分
(Ⅱ)因为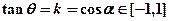 , 所以
, 所以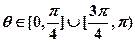 。
。
解析

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
已知直线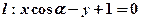 。
。
(Ⅰ)当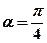 时,求直线
时,求直线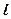 的斜率;
的斜率;
(Ⅱ)若直线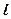
 的倾斜角为
的倾斜角为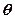 ,求
,求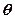 范围。
范围。
解 :(Ⅰ)当
:(Ⅰ)当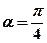 时,
时, ; 3分
; 3分
(Ⅱ)因为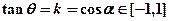 , 所以
, 所以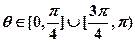 。
。
解析

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案