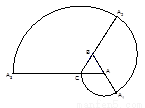题目内容
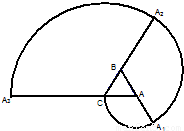
 如图所示的螺旋线是用以下方法画成的,△ABC是边长为1的正三角形,曲线CA1,A1A2,A2A3分别是A,B,C为圆心,AC,BA1,CA2为半径画的弧,曲线CA1A2A3称为螺旋线的第一圈;然后又以A为圆心,AA3半径画弧,如此继续下去,这样画到第n圈.设所得螺旋线CA1A2A3…A3n-2A3n-1A3n的总长度为Sn.求
如图所示的螺旋线是用以下方法画成的,△ABC是边长为1的正三角形,曲线CA1,A1A2,A2A3分别是A,B,C为圆心,AC,BA1,CA2为半径画的弧,曲线CA1A2A3称为螺旋线的第一圈;然后又以A为圆心,AA3半径画弧,如此继续下去,这样画到第n圈.设所得螺旋线CA1A2A3…A3n-2A3n-1A3n的总长度为Sn.求(1)S1=
4π
4π
;(2)Sn=
n(3n+1)π
n(3n+1)π
.分析:(1)当n=1时,即为螺旋线CA1A2A3的长度和,所以S1=
+2×
+3×
=4π
(2)由题知如果这样画到第n圈得到n条螺旋线,是由3n条弧长构成,这些弧长的圆心角都为
,根据弧长公式得到这些弧长是
为首项,
为公差,项数为3n的等差数列,所以这些螺旋线的总长度即为等差数列的前3n的和,求出即可.
| 2π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
(2)由题知如果这样画到第n圈得到n条螺旋线,是由3n条弧长构成,这些弧长的圆心角都为
| 2π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
解答:解:(1)当n=1时,S1=
+2×
+3×
=4π
(2)根据弧长公式知CA1,A1A2,A2A3…A3n-2A3n-1,A3n-1A3n的长度分别为:
,
,…,
,
化简得:
,2×
,3×
,…,3n×
,此数列是
为首项,
为公差,项数为3n的等差数列,则根据等差数列的求和公式得Sn=3n×
+
×
=2nπ+nπ(3n-1)=n(3n+1)π.
故答案为:4π、n(3n+1)π
| 2π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
(2)根据弧长公式知CA1,A1A2,A2A3…A3n-2A3n-1,A3n-1A3n的长度分别为:
| ||
| π |
| ||
| π |
| ||
| π |
化简得:
| 2π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| 3n(3n-1) |
| 2 |
| 2π |
| 3 |
故答案为:4π、n(3n+1)π
点评:本题主要考查了等差数列的性质和数列的求和.解题的关键是归纳总结得到各弧长成等差数列,此题锻炼了学生会经过观察归纳总结得出结论的能力.

练习册系列答案
相关题目
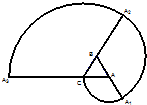 如图所示的螺旋线是用以下方法画成的,△ABC是边长为1的正三角形,曲线CA1,A1A2,A2A3分别是A,B,C为圆心,AC,BA1,CA2为半径画的弧,曲线CA1A2A3称为螺旋线的第一圈;然后又以A为圆心,AA3半径画弧,如此继续下去,这样画到第圈.设所得螺旋线CA1A2A3…A3n-2A3n-1A3n的总长度为Sn,则Sn=
如图所示的螺旋线是用以下方法画成的,△ABC是边长为1的正三角形,曲线CA1,A1A2,A2A3分别是A,B,C为圆心,AC,BA1,CA2为半径画的弧,曲线CA1A2A3称为螺旋线的第一圈;然后又以A为圆心,AA3半径画弧,如此继续下去,这样画到第圈.设所得螺旋线CA1A2A3…A3n-2A3n-1A3n的总长度为Sn,则Sn= 是边长为1的正三角形,曲线
是边长为1的正三角形,曲线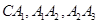 分别是
分别是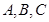 为圆心,
为圆心,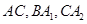 为半径画的弧,曲线
为半径画的弧,曲线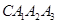 称为螺旋线的第一圈;然后又以A为圆心,
称为螺旋线的第一圈;然后又以A为圆心,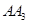 半径画弧,如此继续下去,这样画到第圈。设所得螺旋线
半径画弧,如此继续下去,这样画到第圈。设所得螺旋线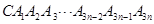 的总长度为
的总长度为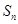 ,则
,则