题目内容
ABC—A1B1C1是各条棱长均为a的正三棱柱,D是侧棱CC1的中点.(1)求证:AB1D⊥平面ABB1A1;
(2)求点C到平面AB1D的距离;
(3)求平面AB1D与平面ABC所成二面角(锐角)的大小.
(1)证明:取AB1中点M,则![]() =
=![]() +
+![]() +
+![]() .?
.?
又![]() =
=![]() +
+![]() +
+![]() ,
,
两式相加可得2![]() =
=![]() +
+![]() =
=![]() +
+![]() .?
.?
由于2![]() ·
·![]() =(
=(![]() +
+![]() )·
)·![]() =0,
=0,
2![]() ·
·![]() =(
=(![]() +
+![]() )·(
)·(![]() -
-![]() )=|
)=|![]() |2-|
|2-|![]() |2=0.
|2=0.
∴DM⊥AA1,DM⊥AB.
∴DM⊥平面ABB1A1,而DM![]() 平面AB1D.
平面AB1D.
∴平面AB1D⊥平面ABB1A1.
(2)解析:一方面A1B⊥DM,另一方面
![]() ·
·![]() =(
=(![]() -
-![]() )·(
)·(![]() +
+![]() )=|
)=|![]() |2-|
|2-|![]() |2=0,
|2=0,
∴A1B⊥AB1.∴A1B⊥平面AB1D.
∴A1B是平面AB1D的法向量.
∴C点到平面AB1D的距离d=|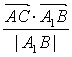 |=
|=![]() =
=![]() =
=![]() .?
.?
(3)解析:平面![]() C的法向量为
C的法向量为![]() ,而平面AB1D的法向量是
,而平面AB1D的法向量是![]() ,设所求二面角为θ(锐角),则
,设所求二面角为θ(锐角),则
|cos(π-θ)|=|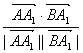 |
|
=|![]() |=
|=![]() =
=![]() .?
.?
∴θ=45°.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
 如图,三棱柱ABC-A1B1C1的侧棱AA2⊥底面ABC,∠ACB=90°,E是棱CC1的中点,F是AB中点,AC=BC=1,AA1=1.
如图,三棱柱ABC-A1B1C1的侧棱AA2⊥底面ABC,∠ACB=90°,E是棱CC1的中点,F是AB中点,AC=BC=1,AA1=1.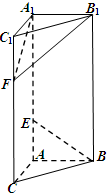 (2013•闵行区二模)如图,在直三棱柱ABC-A1B1C1中,
(2013•闵行区二模)如图,在直三棱柱ABC-A1B1C1中,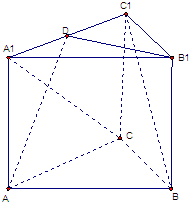 (2008•南京二模)如图,已知正三棱柱ABC-A1B1C1中,AB=
(2008•南京二模)如图,已知正三棱柱ABC-A1B1C1中,AB=