Question

在 DEF中有余弦定理：DE²=DF²+EF²-2DF•EFcosDFE．拓展到空间，类比三角形的余弦定理，写出斜三棱柱ABC-A₁B₁C₁的3个侧面面积与其中两个侧面所成二面角之间的关系式，并予以证明．

Answer 1

分析：利用类比推理边“对应侧面面积”得出结论，证明用到余弦定理平行四边形的面积公式和题中的垂直关系．

解答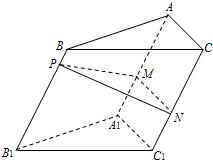：解：在斜三棱柱ABC-A₁B₁C₁中，有 S

2 ABB1A1

=

S

2 BCC1B1

+

S

2 ACC1A1

-2

S

BCC1B1

•

S

ACC1A1

cosα，
其中α为平面CC₁B₁B与平面CC₁A₁A所组成的二面角．
证明：∵CC₁⊥平面PMN，∴上述的二面角为∠MNP，
在△PMN中，PM²=PN²+MN²-2PN•MNcos∠MNP
∴PM²•CC₁²=PN²•CC₁²+MN²•CC₁²-2（PN•CC₁）•（MN•CC₁）cos∠MNP，
∵SBCC1B1=PN•CC₁，SACC1A1=MN•CC₁，SABB1A1=PM•BB₁，
∴S

2 ABB1A1

=

S

2 BCC1B1

+

S

2 ACC1A1

-2

S

BCC1B1

•

S

ACC1A1

cosα，其中α为平面CC₁B₁B与平面CC₁A₁A所组成的二面角．

点评：本题考查了类比推理，证明结论时利用余弦定理，加上适当的变形证出结论．类比的关键是要找准平面中的几何量与空间几何量的对应关系．