题目内容
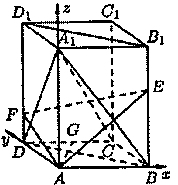
在长方体ABCD-A1B1C1D1中,点E、F分别在B B1、DD1上,且AE⊥A1B,AF⊥A1D.(1)求证:A1C⊥平面AEF;
(2)若规定两个平面所成的角是这两个平面所成的二面角中的锐角(或直角),则在空间中有定理:若两条直线分别垂直于两个平面,则这两条直线所成的角与这两个平面所成的角相等.
试根据上述定理,在AB=4,AD=3,AA1=5时,求平面AEF与平面D1B1BD所成角的大小.(用反三角函数值表示)

答案:
解析:
解析:
| 证明:
(1)因为 由 同理可证 因为 所以 [解](2)过 设 由已知,计算得 如图建立直角坐标系,则得点
因为
由定理知,平面
|

练习册系列答案
相关题目
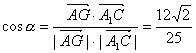 ,
,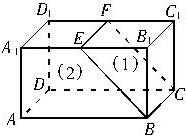 9、如图,在长方体ABCD-A1B1C1D1中,EF∥B1C1,用 平面BCFE把这个长方体分成了(1)、(2)两部分后,这两部分几何体的形状是( )
9、如图,在长方体ABCD-A1B1C1D1中,EF∥B1C1,用 平面BCFE把这个长方体分成了(1)、(2)两部分后,这两部分几何体的形状是( ) 如图,在长方体ABCD-A1B1C1D1中,AA1=AD=a,AB=2a,E、F分别为A1B1、A1D1的中点.
如图,在长方体ABCD-A1B1C1D1中,AA1=AD=a,AB=2a,E、F分别为A1B1、A1D1的中点. 定义:一点到它在一个平面内的正射影的距离叫做这一点到这个平面的距离.如图,在长方体ABCD-A1B1C1D1中,点P是侧面BCC1B1内一动点,若点P到直线C1D1的距离是点P到平面ABCD的距离的
定义:一点到它在一个平面内的正射影的距离叫做这一点到这个平面的距离.如图,在长方体ABCD-A1B1C1D1中,点P是侧面BCC1B1内一动点,若点P到直线C1D1的距离是点P到平面ABCD的距离的 (2013•上海) 如图,在长方体ABCD-A′B′C′D′中,AB=2,AD=1,AA′=1.证明直线BC′平行于平面D′AC,并求直线BC′到平面D′AC的距离.
(2013•上海) 如图,在长方体ABCD-A′B′C′D′中,AB=2,AD=1,AA′=1.证明直线BC′平行于平面D′AC,并求直线BC′到平面D′AC的距离.