Question

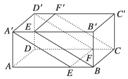
如图所示，在长方体ABCD－A′B′C′D′中，截下一个棱锥C－A′DD′，求棱锥C－A′DD′的体积与剩余部分的体积之比．

Answer 1

[分析]　剩余部分的几何体不是规则几何体，可利用长方体和棱锥的体积之差来求得剩余部分的体积．

[解析]　已知长方体可以看成直四棱柱ADD′A′－BCC′B′.

设它的底面ADD′A′的面积为S，高为h，

则棱锥C－A′DD′的底面积为S，高是h，

故棱锥C－A′DD′的体积为V_{C－A′DD′}＝×Sh＝Sh.

余下的体积是Sh－Sh＝Sh.

所以棱锥C－A′DD′的体积与剩余部分的体积之比为1：5.