题目内容
炮弹运行的轨道是抛物线,现测得我炮位A与目标B的水平距离为6 000米,已知当射程为6 000米时,炮弹运行的最大高度是1 200米,在A、B之间距离A点500米处有一高达350米的障碍物,试确定炮弹可否安全越过此障碍物.
点C在抛物线的下方,故炮弹可安全通过此障碍物.
解析:
建立如图所示的坐标系,B(3 000,-1 200).障碍物顶点C(-2 500,-850),下面判断点C与抛物线的位置关系,设抛物线方程为x2=-2py(p>0).
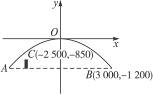
∴3 0002=-2p×(-1 200).∴p=3 750.
∴抛物线方程为x2=-7 500y,令x=-2 500,可得y=-![]() >-850.
>-850.
∴点C在抛物线的下方,故炮弹可安全通过此障碍物.

练习册系列答案
相关题目