题目内容
某跨国饮料公司对全世界所有人均GDP(即人均纯收入)在0.5—8千美元的地区销售,该公司M饮料的销售情况的调查中发现:人均GDP处在中等的地区对该饮料的销售量最多,然后向两边递减.
(1)下列几个模拟函数中(x表示人均GDP,单位:千美元;y表示年人均M饮料的销量,单位:升),用哪个来描述人均,饮料销量与地区的人均GDP的关系更合适?说明理由.
(A) (B)
(B) 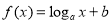 (C)
(C)  (D)
(D) 
(2)若人均GDP为1千美元时,年人均M饮料的销量为2升;人均GDP为4千美元时,年人均M饮料的销量为5升;把你所选的模拟函数求出来.;
(3)因为M饮料在N国被检测出杀虫剂的含量超标,受此事件影响,M饮料在人均GDP不高于3千美元的地区销量下降5%,不低于6千美元的地区销量下降5%,其他地区的销量下降10%,根据(2)所求出的模拟函数,求在各个地区中,年人均M饮料的销量最多为多少?
(1)A;(2) (
( );(3)参考解析
);(3)参考解析
【解析】
试题分析:(1)因为人均GDP处在中等的地区对该饮料的销售量最多,然后向两边递减,所以相应的图像应该是先增后减的形式.有因为B,C,D选项分别代表对数函数,指数函数,幂函数,它们在定义域内都是单调的.所以这三种模型不成立.故选A模型.
(2)由(1)得模型函数为A的二次函数.所以根据已给的两个条件可以分别求出 的值.即可求得所选的模拟函数.
的值.即可求得所选的模拟函数.
(3)由(2)所得的销量的关系式可得,再依据三段不同的影响情况所得的解析式求出对应的年人均M饮料的销量最大值即可.
试题解析:(1)因为 表示的函数在区间 [0.5,8]上是单调的,所以用
表示的函数在区间 [0.5,8]上是单调的,所以用 来模拟比较合适.
来模拟比较合适.
2分
(2)因为人均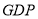 为
为 千美元时,年人均
千美元时,年人均 饮料的销售量为
饮料的销售量为 升;若人均
升;若人均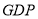 为
为 千美元时,年人均
千美元时,年人均 饮料的销售量为
饮料的销售量为 升,把
升,把 代入(
代入( )函数
)函数 ,得
,得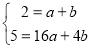 ,解得
,解得
所以所求函数的解析式为 (
( ) 7分
) 7分
(3)根据题意可得:
当 时,
时, ,在
,在 上递增,
上递增,
则当 时,
时, ;
;
当 时,
时, ,
, ,则当
,则当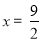 时,
时, ;
;
当 时,
时, ,在
,在 上递减,
上递减,
则当 时,
时, ;
;
显然 ,
,
所以当人均 在
在 千美元的地区,人均
千美元的地区,人均 饮料的销量最多为
饮料的销量最多为 升. 12分
升. 12分
考点:1.归纳类比的思想.2.待定系数的思想.3.分类讨论求最值的问题.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案