题目内容
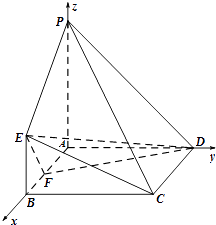
【题目】在如图所示的几何体中,四边形ABCD为正方形,PA⊥平面ABCD,PA∥BE,AB=PA=4,BE=2. 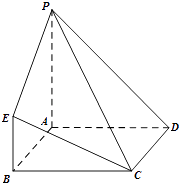
(1)求证:CE∥平面PAD;
(2)求PD与平面PCE所成角的正弦值;
(3)在棱AB上是否存在一点F,使得平面DEF⊥平面PCE?如果存在,求 ![]() 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
【答案】
(1)证明:设PA中点为G,连结EG,DG.
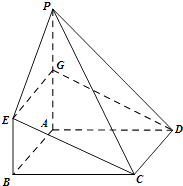
因为PA∥BE,且PA=4,BE=2,
所以BE∥AG且BE=AG,
所以四边形BEGA为平行四边形.
所以EG∥AB,且EG=AB.
因为正方形ABCD,所以CD∥AB,CD=AB,
所以EG∥CD,且EG=CD.
所以四边形CDGE为平行四边形.
所以CE∥DG.
因为DG平面PAD,CE平面PAD,
所以CE∥平面PAD.
(2)解:如图建立空间坐标系,
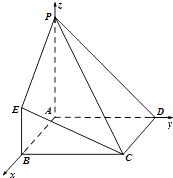
则B(4,0,0),C(4,4,0),
E(4,0,2),P(0,0,4),D(0,4,0),
所以 ![]() =(4,4,﹣4),
=(4,4,﹣4), ![]() =(4,0,﹣2),
=(4,0,﹣2), ![]() =(0,4,﹣4).
=(0,4,﹣4).
设平面PCE的一个法向量为 ![]() =(x,y,z),
=(x,y,z),
所以 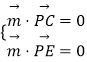 ,可得
,可得 ![]() .
.
令x=1,则 ![]() ,所以
,所以 ![]() =(1,1,2).
=(1,1,2).
设PD与平面PCE所成角为a,
则sinα=|cos< ![]() ,
, ![]() >|=|
>|=| 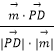 =|
=| ![]() |=
|= ![]() ..
..
所以PD与平面PCE所成角的正弦值是 ![]() .
.
(3)解:依题意,可设F(a,0,0),则 ![]() ,
, ![]() =(4,﹣4,2).
=(4,﹣4,2).
设平面DEF的一个法向量为 ![]() =(x,y,z),
=(x,y,z),
则 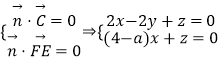 .
.
令x=2,则 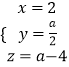 ,
,
所以 ![]() =(2,
=(2, ![]() ,a﹣4).
,a﹣4).
因为平面DEF⊥平面PCE,
所以 ![]()
![]() =0,即2+
=0,即2+ ![]() +2a﹣8=0,
+2a﹣8=0,
所以a= ![]() <4,点
<4,点 ![]() .
.
所以 ![]() .
.
【解析】(1)设PA中点为G,连结EG,DG,可证四边形BEGA为平行四边形,又正方形ABCD,可证四边形CDGE为平行四边形,得CE∥DG,由DG平面PAD,CE平面PAD,即证明CE∥平面PAD.(2)如图建立空间坐标系,设平面PCE的一个法向量为 ![]() =(x,y,z),由
=(x,y,z),由 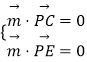 ,令x=1,则可得
,令x=1,则可得 ![]() =(1,1,2),设PD与平面PCE所成角为a,由向量的夹角公式即可得解.(3)设平面DEF的一个法向量为
=(1,1,2),设PD与平面PCE所成角为a,由向量的夹角公式即可得解.(3)设平面DEF的一个法向量为 ![]() =(x,y,z),由
=(x,y,z),由 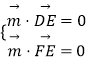 ,可得
,可得 ![]() ,由
,由 ![]()
![]() =0,可解a,然后求得
=0,可解a,然后求得 ![]() 的值.
的值.
【考点精析】本题主要考查了直线与平面平行的判定和空间角的异面直线所成的角的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则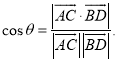 才能正确解答此题.
才能正确解答此题.

 阅读快车系列答案
阅读快车系列答案