题目内容
【题目】四棱锥S﹣ABCD的底面ABCD是正方形,各侧棱长与底面的边长均相等,M为SA的中点,则直线BM与SC所成的角的余弦值为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】C
【解析】解:过点P作PO⊥平面ABCD,交ABCD于点O,
以O为原点,过O作DA的平行线为x轴,过O作AB的平行线为y轴,OS为z轴,建立空间直角坐标系,
如图所示:
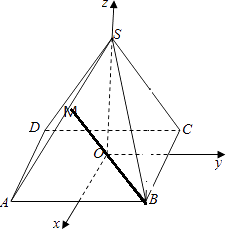
设正四棱锥S﹣ABCD侧棱长与底面边长都为2,
则A(1,﹣1,0),OB= ![]() ,OS=
,OS= ![]() =
= ![]() ,B(1,1,0),
,B(1,1,0),
S(0,0, ![]() ),C(﹣1,1,0),M(
),C(﹣1,1,0),M( ![]() ,﹣
,﹣ ![]() ,
, ![]() ),
),
![]() =(﹣
=(﹣ ![]() ,﹣
,﹣ ![]() ,
, ![]() ),
), ![]() =(﹣1,1,﹣
=(﹣1,1,﹣ ![]() ),
),
设BE与SA所成角为θ,
则cosθ= 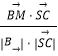 =
= ![]() .
.
∴BM与SC所成角的余弦值为 ![]() .
.
所以答案是:C.
【考点精析】认真审题,首先需要了解异面直线及其所成的角(异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系).

练习册系列答案
相关题目