题目内容
已知曲线C上任一点P到直线x=1与点F(-1,0)的距离相等.(1)求曲线C的方程;
(2)设直线y=x+b与曲线C交于点A,B,问在直线l:y=2上是否存在与b无关的定点M,使得直线MB与MA关于直线l对称,若存在,求出点M的坐标,若不存在,请说明理由.
【答案】分析:(1)根据抛物线的定义可知点F(-1,0)为抛物线的焦点,x=1为其准线,设出抛物线的方程,根据焦点坐标求得p,则抛物线方程可得.
(2)设A(x1,y1),B(x2,y2),假设存在点M(a,2)满足条件,根据题意可推断出kAM+kBM=0,把A,B坐标代入,同时根据抛物线方程可知x1和y1,x2和y2的关系,把直线与抛物线方程联立消去x,利用韦达定理表示出y1+y2和y1y2,代入方程③中,求得a的值,推断出出存在点M(-1,2)满足题意.
解答:解:(1)依题意,曲线C为抛物线,且点F(-1,0)为抛物线的焦点,x=1为其准线,
则抛物线形式为y2=-2px,由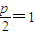 ,得p=2,
,得p=2,
则曲线C的方程为y2=-4x.
(2)设A(x1,y1),B(x2,y2),假设存在点M(a,2)满足条件,则kAM+kBM=0
即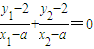 ,即x2y1+x1y2-2(x1+x2)-a(y1+y2)=0①
,即x2y1+x1y2-2(x1+x2)-a(y1+y2)=0①
而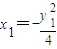 ,
,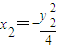 ,②
,②
整理得y1y2(y1+y2)+4a(y1+y2)-2(y12+y22)-16a=0,
即为:y1y2(y1+y2)+4a(y1+y2)-2[(y1+y2)2-2y1y2]-16a=0,③
由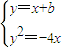 得:y2+4y-4b=0,
得:y2+4y-4b=0,
则y1+y2=-4,y1y2=-4b,④
将④代入③得:-4b×(-4)+4a×(-4)-2[(-4)2+8b]-16a=0,即a=-1.
因此,存在点M(-1,2)满足题意.
点评:本题主要考查了抛物线的简单性质,直线与抛物线的关系,抛物线的标准方程.考查了学生分析问题和运算能力的.
(2)设A(x1,y1),B(x2,y2),假设存在点M(a,2)满足条件,根据题意可推断出kAM+kBM=0,把A,B坐标代入,同时根据抛物线方程可知x1和y1,x2和y2的关系,把直线与抛物线方程联立消去x,利用韦达定理表示出y1+y2和y1y2,代入方程③中,求得a的值,推断出出存在点M(-1,2)满足题意.
解答:解:(1)依题意,曲线C为抛物线,且点F(-1,0)为抛物线的焦点,x=1为其准线,
则抛物线形式为y2=-2px,由
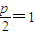 ,得p=2,
,得p=2,则曲线C的方程为y2=-4x.
(2)设A(x1,y1),B(x2,y2),假设存在点M(a,2)满足条件,则kAM+kBM=0
即
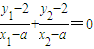 ,即x2y1+x1y2-2(x1+x2)-a(y1+y2)=0①
,即x2y1+x1y2-2(x1+x2)-a(y1+y2)=0①而
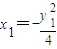 ,
,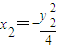 ,②
,②整理得y1y2(y1+y2)+4a(y1+y2)-2(y12+y22)-16a=0,
即为:y1y2(y1+y2)+4a(y1+y2)-2[(y1+y2)2-2y1y2]-16a=0,③
由
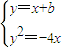 得:y2+4y-4b=0,
得:y2+4y-4b=0,则y1+y2=-4,y1y2=-4b,④
将④代入③得:-4b×(-4)+4a×(-4)-2[(-4)2+8b]-16a=0,即a=-1.
因此,存在点M(-1,2)满足题意.
点评:本题主要考查了抛物线的简单性质,直线与抛物线的关系,抛物线的标准方程.考查了学生分析问题和运算能力的.

练习册系列答案
相关题目