题目内容
(本小题满分12分)
已知函数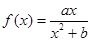 在
在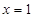 处取得极值为2,设函数
处取得极值为2,设函数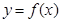 图象上任意一点
图象上任意一点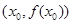 处的切线斜率为k。
处的切线斜率为k。
(1)求k的取值范围;
(2)若对于任意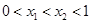 ,存在k,使得
,存在k,使得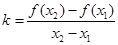 ,求证:
,求证: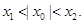
【答案】
(Ⅰ)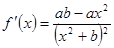
由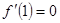 及
及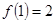 得,
得,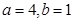 (2分)
(2分)
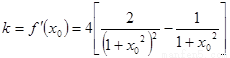
设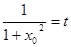 ,
,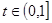 得
得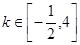 (4分)
(4分)
(Ⅱ)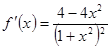 ,令
,令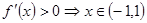
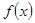 的增区间为
的增区间为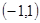 ,故当
,故当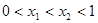 时,
时, .
.
即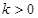 ,故
,故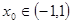 (6分)
(6分)
(法一)由于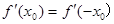 ,故只需要证明
,故只需要证明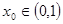 时结论成立
时结论成立
由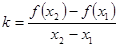 ,得
,得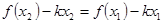 ,
,
记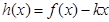 ,则
,则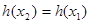
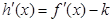 ,则
,则 ,
,
设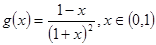 ,
,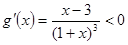 ,
,
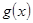 为减函数,故
为减函数,故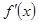 为减函数
为减函数
故当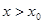 时有
时有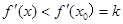 ,此时
,此时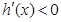 ,
,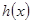 为减函数
为减函数
当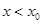 时
时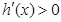 ,
,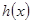 为增函数
为增函数
所以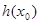 为
为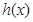 的唯一的极大值,因此要使
的唯一的极大值,因此要使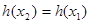 ,必有
,必有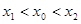
综上,有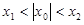 成立
(12分)
成立
(12分)
(法二) 由已知: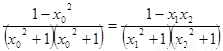 ①
①
下面以反证法证明结论:
假设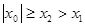 ,则
,则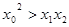 ,
,
因为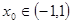 ,
,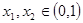 ,所以
,所以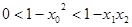 ,
,
又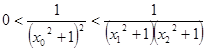 ,故
,故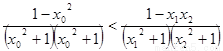
与①式矛盾
假设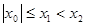 ,同理可得
,同理可得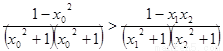
与①式矛盾
综上,有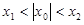 成立
(12分)
成立
(12分)
【解析】略

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目