题目内容
如图,圆柱OO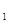 内有一个三棱柱ABC—A
内有一个三棱柱ABC—A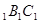 ,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径。
,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径。
(1)证明:平面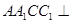 平面
平面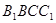 ;
;
(2)设AB=AA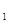
 ,在圆柱OO
,在圆柱OO 内随机选取一点,记该点取自三棱柱ABC—A
内随机选取一点,记该点取自三棱柱ABC—A B
B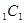
 内的概率为P.
内的概率为P.
①当点C在圆周上运动时,求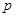 的最大值;
的最大值;
②记平面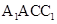 与平面
与平面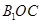 所成的角为
所成的角为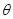
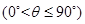 ,当
,当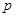 取最大值时,求
取最大值时,求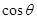 的值。
的值。

【答案】
(1)因为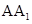
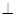 平面ABC,
平面ABC,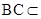 平面ABC,所以
平面ABC,所以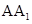
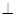
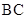 ,
,
因为AB是圆O直径,所以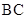
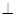
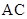 ,又
,又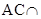
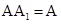 ,所以
,所以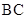
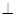 平面
平面 ,
,
而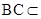 平面
平面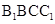 ,所以平面
,所以平面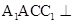 平面
平面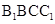 。
。
(2)(i)设圆柱的底面半径为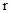 ,则AB=
,则AB=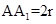 ,故三棱柱
,故三棱柱 的体积为
的体积为
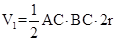 =
=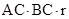 ,又因为
,又因为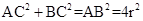 ,
,
所以 =
=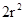 ,当且仅当
,当且仅当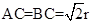 时等号成立,
时等号成立,
从而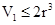 ,而圆柱的体积
,而圆柱的体积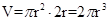 ,
,
故 =
=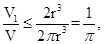 当且仅当
当且仅当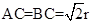 ,即
,即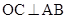 时等号成立,
时等号成立,
所以 的最大值是
的最大值是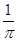 。
。
(ii)由(i)可知, 取最大值时,
取最大值时,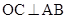 ,于是以O为坐标原点,建立空间直角坐标系
,于是以O为坐标原点,建立空间直角坐标系 (如图),则C(r,0,0),B(0,r,0),
(如图),则C(r,0,0),B(0,r,0), (0,r,2r),
(0,r,2r),
因为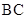
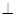 平面
平面 ,所以
,所以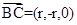 是平面
是平面 的一个法向量,
的一个法向量,
设平面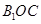 的法向量
的法向量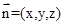 ,由
,由 ,故
,故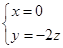 ,
,
取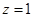 得平面
得平面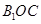 的一个法向量为
的一个法向量为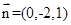 ,因为
,因为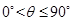 ,
,
所以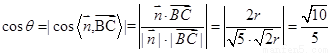 。
。
【解析】略

练习册系列答案
相关题目
 如图,圆柱OO1内有一个三棱柱ABC-A1B1C1,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O的直径.
如图,圆柱OO1内有一个三棱柱ABC-A1B1C1,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O的直径. 如图,圆柱OO1内有一个三棱柱ABC-A1B1C1,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O的直径.
如图,圆柱OO1内有一个三棱柱ABC-A1B1C1,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O的直径. 如图,圆柱OO1内有一个三棱柱ABC-A1B1C1,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径,AA1=AC=CB=2.
如图,圆柱OO1内有一个三棱柱ABC-A1B1C1,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径,AA1=AC=CB=2.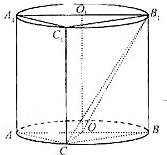 如图,圆柱OO1内有一个三棱柱ABC-A1B1C1,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径.
如图,圆柱OO1内有一个三棱柱ABC-A1B1C1,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径.