题目内容
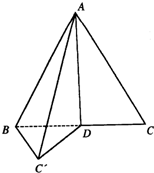如图所示，等边△ABC的边长为4，D为BC中点，沿AD把△ADC折叠到△ADC′处，使二面角B-AD-C′为60°，则折叠后点A到直线BC′的距离为分析：由二面角的平面角的概念可知：∠BDC′即为二面角B-AD-C′的平面角，有∠BDC′=60°，所以BC′=2，作DM⊥BC′于点M，连接AM，则AM为点A到直线BC′的距离，二面角A-BC′-D的平面角即为∠AMD．
解答：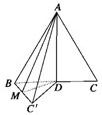
解：如图，作DM⊥BC′于点M，连接AM，则AM为点A到直线BC′的距离，
AD=2
，DM=
，所以AM=
=
．
二面角A-BC′-D的平面角为∠AMD，
正切值为tan∠AMD=
=2；
故答案为
，2．
解：如图，作DM⊥BC′于点M，连接AM，则AM为点A到直线BC′的距离，AD=2
| 3 |
| 3 |
| AD2+DM2 |
| 15 |
二面角A-BC′-D的平面角为∠AMD，
正切值为tan∠AMD=
2
| ||
|
故答案为
| 15 |
点评：本小题主要考查空间线面关系、二面角的度量等知识，考查数形结合、化归与转化的数学思想方法，以及空间想象能力、推理论证能力和运算求解能力
练习册系列答案
名校课堂系列答案
相关题目
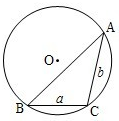通常用a、b、c表示△ABC的三个内角∠A、∠B、∠C所对边的边长，R表示△ABC外接圆半径．
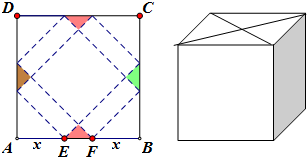请你设计一个包装盒，如图所示，ABCD是边长为60cm的正方形硬纸片，切去阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起，使得A，B，C，D四个点重合于图中的点P，正好形成一个正四棱柱形状的包装盒，E、F在AB上，是被切去的等腰直角三角形斜边的两个端点，设AE=FB=x（cm）．
(a1
(a1