题目内容
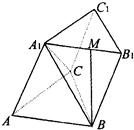 如图,三棱柱ABC-A1B1C1的底面是边长为a的正三角形,侧面ABB1A1是菱形且垂直于底面,∠A1AB=60°,M是A1B1的中点.
如图,三棱柱ABC-A1B1C1的底面是边长为a的正三角形,侧面ABB1A1是菱形且垂直于底面,∠A1AB=60°,M是A1B1的中点.(1)求证:BM⊥AC;
(2)求二面角B-B1C1-A1的正切值.
分析:(1)先根据ABB1A1是菱形,∠A1AB=60°得到△A1B1B是正三角形,则BM⊥A1B,然后根据平面ABB1A1与平面A1B1C1垂直的性质性质定理可知BM⊥平面A1B1C1,而AC∥A1C1,从而得到结论;
(2)根据题意可知BE⊥B1C1,根据二面角平面角的定义可知∠BEM为所求二面角的平面角,在△A1B1C1中,求出ME,在Rt△BMB1中,求出MB,最后在三角形BEM中求二面角的正切值.
(2)根据题意可知BE⊥B1C1,根据二面角平面角的定义可知∠BEM为所求二面角的平面角,在△A1B1C1中,求出ME,在Rt△BMB1中,求出MB,最后在三角形BEM中求二面角的正切值.
解答:解:(1)证明:∵ABB1A1是菱形,∠A1AB=60°?△A1B1B是正三角形
又∵
,∴ BM⊥A1B?BM⊥平面A1B1C1
?BM⊥AC
(2)
?BE⊥B1C1∴∠BEM为所求二面角的平面角
△A1B1C1中,ME=MB1•sin60°=
a,Rt△BMB1中,MB=MB1•tan60°=
a
∴tan∠BEM=
=2,∴所求二面角的正切值是2
又∵
|
|
(2)
|
△A1B1C1中,ME=MB1•sin60°=
| ||
| 4 |
| ||
| 2 |
∴tan∠BEM=
| MB |
| ME |
点评:本题主要考查了直线与平面垂直的判定,以及二面角的度量,求二面角,关键是构造出二面角的平面角,常用的方法有利用三垂线定理和通过求法向量的夹角,然后再将其转化为二面角的平面角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,D、E分别为AA1、B1C的中点,AB=AC.
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,D、E分别为AA1、B1C的中点,AB=AC. (2012•黑龙江)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=
(2012•黑龙江)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC= 如图,三棱柱ABC-A1B1C1的底面ABC为正三角形,侧棱AA1⊥平面ABC,D是BC中点,且AA1=AB
如图,三棱柱ABC-A1B1C1的底面ABC为正三角形,侧棱AA1⊥平面ABC,D是BC中点,且AA1=AB (2012•大连二模)如图,三棱柱ABC-A′B′C′,cc′=
(2012•大连二模)如图,三棱柱ABC-A′B′C′,cc′=