题目内容
 (2012•大连二模)如图,三棱柱ABC-A′B′C′,cc′=
(2012•大连二模)如图,三棱柱ABC-A′B′C′,cc′=| 2 |
| 2 |
(I)求证:EF∥平面A′BC′;
(Ⅱ)若AC≤
| 2 |
| ||
| 3 |
分析:(I)法一:利用直线与平面平行的判定定理证明EF∥平面A′BC′;
法二:通过建立空间直角坐标系,求出平面A'BC'的法向量,利用向量数量积为证明直线与平面平行.
(Ⅱ)利用走法二的空间直角坐标系,求出平面ACC'A'的法向量,利用EF与平面ACC'A'所成的角的余弦为
,求出b的值,然后求出平面AA'B的一个法向量,利用向量的数量积求二面角C-AA'-B的大小.
法二:通过建立空间直角坐标系,求出平面A'BC'的法向量,利用向量数量积为证明直线与平面平行.
(Ⅱ)利用走法二的空间直角坐标系,求出平面ACC'A'的法向量,利用EF与平面ACC'A'所成的角的余弦为
| ||
| 3 |
解答: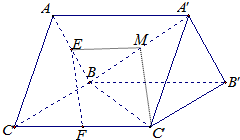 解:(Ⅰ)证法一:取A'B中点M,连接EM、C'M,
解:(Ⅰ)证法一:取A'B中点M,连接EM、C'M,
又∵E为AB中点,∴EM
AA′
∵AA′
BB′
CC′,
F为CC'中点,∴FC′
AA′,
∴FC′
EM∴EMCF是平行四边形,
∴EF∥C'M,…(2分)
又EF?平面A'BC',C'M?平面A'BC',∴EF∥平面A'BC'…(4分)
证法二: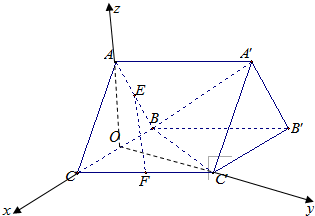
∴△CC′B是以BC为斜边的等腰直角三角形.
取BC中点O,连接AO、C'O有AO⊥BC,C'O⊥BC
∵面ABC⊥面BCC'B',且面ABC∩面BCC'B'=BC
∴AO⊥面BCC'B',C'O⊥面ABC
如图建立空间直角坐标系O-xyz∴C(1,0,0),C'(0,10),A(0,0,b),B(-1,0,0)(b>0)
∴E(-
,0,
),F(
,
,0),∴
=(1,
,-
)
设平面A'BC'的法向量为
=(x,y,z)
又
=(1,1,0),
=
=(1,0,-b)
∴
∴
的一组解为
=(b,-b,1)
∴
•
=b-
-
=0
∴
⊥
又EF?平面A'BC'∴EF∥平面A'BC'…(4分)
(Ⅱ)解:利用(Ⅰ)中证法二的坐标系,设平面ACC'A'的法向量为
=(x,y,z)
又
=(-1,1,0),
=(1,0,-b)
∴
∴
1的一组解为
1=(b,b,1)…(5分)
又
=(1,
,-
)
∴
=
=
…(6分)
解得b=1,b=
∵AC≤
∴b=1…(8分)
同理可求平面AA'B的一个法向量
2=(1,1,-1)
∴cos<
•
>=
…(11分)
所以所求二面角的大小为arccos
.…(12分)
 解:(Ⅰ)证法一:取A'B中点M,连接EM、C'M,
解:(Ⅰ)证法一:取A'B中点M,连接EM、C'M,又∵E为AB中点,∴EM
| ||
. |
| 1 |
| 2 |
∵AA′
| ||
. |
| ||
. |
F为CC'中点,∴FC′
| ||
. |
| 1 |
| 2 |
∴FC′
| ||
. |
∴EF∥C'M,…(2分)
又EF?平面A'BC',C'M?平面A'BC',∴EF∥平面A'BC'…(4分)
证法二:

|
∴△CC′B是以BC为斜边的等腰直角三角形.
取BC中点O,连接AO、C'O有AO⊥BC,C'O⊥BC
∵面ABC⊥面BCC'B',且面ABC∩面BCC'B'=BC
∴AO⊥面BCC'B',C'O⊥面ABC
如图建立空间直角坐标系O-xyz∴C(1,0,0),C'(0,10),A(0,0,b),B(-1,0,0)(b>0)
∴E(-
| 1 |
| 2 |
| b |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| EF |
| 1 |
| 2 |
| b |
| 2 |
设平面A'BC'的法向量为
| n |
又
| BC′ |
| A′C′ |
| AC |
∴
|
| n |
| n |
∴
| n |
| EF |
| b |
| 2 |
| b |
| 2 |
∴
| n |
| EF |
又EF?平面A'BC'∴EF∥平面A'BC'…(4分)
(Ⅱ)解:利用(Ⅰ)中证法二的坐标系,设平面ACC'A'的法向量为
| n1 |
又
| CC′ |
| AC |
∴
|
| n |
| n |
又
| EF |
| 1 |
| 2 |
| b |
| 2 |
∴
|
| ||||
|
|
| b | ||||||||
|
| ||
| 3 |
解得b=1,b=
| ||
| 2 |
| 2 |
同理可求平面AA'B的一个法向量
| n |
∴cos<
| n1 |
| n2 |
| 1 |
| 3 |
所以所求二面角的大小为arccos
| 1 |
| 3 |
点评:本题考查直线与平面平行的判定定理的应用,利用向量的垂直关系以及向量的数量积求解直线与平面所成角以及二面角,考查计算能力.

练习册系列答案
相关题目
 (2012•大连二模)已知程序框图如图所示,则输出的s为( )
(2012•大连二模)已知程序框图如图所示,则输出的s为( )