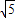题目内容
已知A、B是直线l上任意两点,O是l外一点,若l上一点C满足
=cosθ
+cos2θ
,则sin2θ+sin4θ+sin6θ=( )
| OC |
| OA |
| OB |
分析:根据A、B、C三点共线,结合题中向量等式得到cosθ+cos2θ=1,从而cosθ=1-cos2θ=sin2θ,由此化简得sin2θ+sin4θ+sin6θ=1+cosθ-cos2θ,再由cosθ+cos2θ=1解出cosθ和cos2θ的值,代入即可得到所求的值.
解答:解:∵A、B、C三点在同一条直线l上
∴由
=cosθ
+cos2θ
,得cosθ+cos2θ=1
因此,cosθ=1-cos2θ=sin2θ,
∴sin2θ+sin4θ+sin6θ=cosθ+cos2θ+cos3θ
结合cosθ+cos2θ=1,
得sin2θ+sin4θ+sin6θ=1+cos3θ=1+cosθ(1-cosθ)=1+cosθ-cos2θ
由cosθ+cos2θ=1解出cosθ=
,得cos2θ=
∴sin2θ+sin4θ+sin6θ=1+
-
=-1+
故选:B
∴由
| OC |
| OA |
| OB |
因此,cosθ=1-cos2θ=sin2θ,
∴sin2θ+sin4θ+sin6θ=cosθ+cos2θ+cos3θ
结合cosθ+cos2θ=1,
得sin2θ+sin4θ+sin6θ=1+cos3θ=1+cosθ(1-cosθ)=1+cosθ-cos2θ
由cosθ+cos2θ=1解出cosθ=
| ||
| 2 |
3-
| ||
| 2 |
∴sin2θ+sin4θ+sin6θ=1+
| ||
| 2 |
3-
| ||
| 2 |
| 5 |
故选:B
点评:本题给出向量含有三角函数系数的等式,求三角函数式的值.着重考查了向量的线性运算和同角三角函数基本关系等知识,属于中档题.

练习册系列答案
相关题目
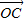 =cosθ
=cosθ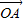 +cos2θ
+cos2θ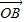 ,则sin2θ+sin4θ+sin6θ=( )
,则sin2θ+sin4θ+sin6θ=( )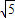
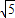
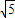 或1+
或1+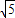
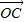 =cosθ
=cosθ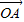 +cos2θ
+cos2θ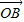 ,则sin2θ+sin4θ+sin6θ=( )
,则sin2θ+sin4θ+sin6θ=( )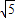
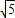
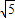 或1+
或1+