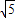题目内容
已知A、B是直线l上任意两点,O是l外一点,若l上一点C满足
=
cosθ+
cos2θ,则sinθ+sin2θ+sin4θ+sin6θ的最大值是( )
| OC |
| OA |
| OB |
A.
| B.
| C.
| D.
|
∵A、B、C 共线,
∴由
=
cosθ+
cos2θ,
得 cosθ+(cosθ)2=1,(三点共线的充要条件)
∴(cosθ)2=1-cosθ,
cosθ=1-(cosθ)2=(sinθ)2,
且(cosθ)3=cosθ(cosθ)2
=cosθ(1-cosθ)
=cosθ-(cosθ)2
=cosθ-(1-cosθ)
=2cosθ-1,
∴sinθ+(sinθ)2+(sinθ)4+(sinθ)6
=sinθ+cosθ+(cosθ)2+(cosθ)3
=sinθ+cosθ+(1-cosθ)+(2cosθ-1)
=sinθ+2cosθ
因此,sinθ+sin2θ+sin4θ+sin6θ的最大值=
=
.
故选C.
∴由
| OC |
| OA |
| OB |
得 cosθ+(cosθ)2=1,(三点共线的充要条件)
∴(cosθ)2=1-cosθ,
cosθ=1-(cosθ)2=(sinθ)2,
且(cosθ)3=cosθ(cosθ)2
=cosθ(1-cosθ)
=cosθ-(cosθ)2
=cosθ-(1-cosθ)
=2cosθ-1,
∴sinθ+(sinθ)2+(sinθ)4+(sinθ)6
=sinθ+cosθ+(cosθ)2+(cosθ)3
=sinθ+cosθ+(1-cosθ)+(2cosθ-1)
=sinθ+2cosθ
因此,sinθ+sin2θ+sin4θ+sin6θ的最大值=
| 1+4 |
| 5 |
故选C.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
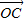 =cosθ
=cosθ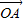 +cos2θ
+cos2θ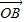 ,则sin2θ+sin4θ+sin6θ=( )
,则sin2θ+sin4θ+sin6θ=( )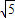
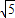
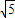 或1+
或1+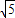
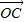 =cosθ
=cosθ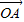 +cos2θ
+cos2θ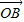 ,则sin2θ+sin4θ+sin6θ=( )
,则sin2θ+sin4θ+sin6θ=( )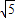
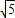
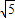 或1+
或1+