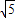题目内容
已知A、B是直线l上任意两点,O是l外一点,若l上一点C满足
=
cosθ+
cos2θ,则sin2θ+sin4θ+sin6θ的值是 .
| OC |
| OA |
| OB |
分析:依题意知,cosθ+cos2θ=1,于是得cosθ=sin2θ,sin6θ=2cosθ-1,sin2θ+sin4θ+sin6θ=2cosθ,解方程cosθ+cos2θ=1,可求得cosθ,从而可得答案.
解答:解:∵A、B、C三点共线,且
=
cosθ+
cos2θ,
∴cosθ+cos2θ=1,(三点共线的充要条件)
∴cos2θ=1-cosθ,
∴cosθ=1-cos2θ=sin2θ,
∴sin6θ=cos3θ=cosθ•(1-sin2θ)=cosθ(1-cosθ)=cosθ-cos2θ=cosθ-(1-cosθ)=2cosθ-1,
∴sin2θ+sin4θ+sin6θ
=cosθ+cos2θ+2cosθ-1
=cosθ+1-cosθ+2cosθ-1
=2cosθ,
由cos2θ=1-cosθ得cosθ=
或cosθ=
<-1,舍去,
∴cosθ=
,
∴原式=2cosθ=
-1,
故答案为:
-1.
| OC |
| OA |
| OB |
∴cosθ+cos2θ=1,(三点共线的充要条件)
∴cos2θ=1-cosθ,
∴cosθ=1-cos2θ=sin2θ,
∴sin6θ=cos3θ=cosθ•(1-sin2θ)=cosθ(1-cosθ)=cosθ-cos2θ=cosθ-(1-cosθ)=2cosθ-1,
∴sin2θ+sin4θ+sin6θ
=cosθ+cos2θ+2cosθ-1
=cosθ+1-cosθ+2cosθ-1
=2cosθ,
由cos2θ=1-cosθ得cosθ=
-1+
| ||
| 2 |
-1-
| ||
| 2 |
∴cosθ=
-1+
| ||
| 2 |
∴原式=2cosθ=
| 5 |
故答案为:
| 5 |
点评:本题考查三角函数中的恒等变换应用,求得,sin6θ=2cosθ-1,sin2θ+sin4θ+sin6θ=2cosθ是关键,也是难点,考查转化思想与运算能力,属于难题.

练习册系列答案
相关题目
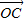 =cosθ
=cosθ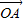 +cos2θ
+cos2θ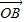 ,则sin2θ+sin4θ+sin6θ=( )
,则sin2θ+sin4θ+sin6θ=( )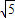
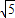
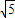 或1+
或1+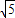
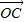 =cosθ
=cosθ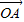 +cos2θ
+cos2θ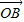 ,则sin2θ+sin4θ+sin6θ=( )
,则sin2θ+sin4θ+sin6θ=( )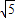
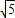
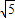 或1+
或1+