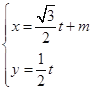题目内容
【题目】某少数民族的刺绣有着悠久的历史，图中（1）、（2）、（3）、（4）为她们刺锈最简单的四个图案，这些图案都是由小正方向构成，小正方形数越多刺锈越漂亮，向按同样的规律刺锈（小正方形的摆放规律相同），设第
个图形包含
个小正方形
（1）求
的值
（2）求出
的表达式
（3）求证：当
时， 
【答案】（1）61（2）f（n）=2n2﹣2n+1；（3）见解析
【解析】试题分析：（1）根据列举法找规律，得到
的值；（2）同样根据列举法找规律
，根据累加法得到
的表达式；（3）根据（2）的结果，代入可得
，利用累加法求和，再根据数列的单调性证明不等式.
试题解析：解：（1）f（1）=1，f（2）=1+4=5，
f（3）=1+4+8=13，f（4）=1+4+8+12=25，
f（5）=1+4+8+12+16=41．f（6）=1+4+8+12+16+20=61；
（2）∵f（2）﹣f（1）=4=4×1，
f（3）﹣f（2）=8=4×2，
f（4）﹣f（3）=12=4×3，
f（5）﹣f（4）=16=4×4，
由上式规律得出f（n+1）﹣f（n）=4n．
∴f（n）﹣f（n﹣1）=4（n﹣1），
f（n﹣1）﹣f（n﹣2）=4（n﹣2），
f（n﹣2）﹣f（n﹣3）=4（n﹣3），
…
f（2）﹣f（1）=4×1，
∴f（n）﹣f（1）=4[（n﹣1）+（n﹣2）+…+2+1]
=2（n﹣1）n，
∴f（n）=2n2﹣2n+1；
（2）证明：当n≥2时，
=
=
（
﹣
），
∴
+
+
+…+
=1+
（1﹣+﹣
+…+
﹣
）
=1+（1﹣
）=
﹣
．
由于g（n）=﹣为递增数列，
即有g（n）≥g（1）=1，
且g（n）＜，
则
+
+
+…+
＜
成立．
练习册系列答案
相关题目
