题目内容
12.圆x2+y2-2x-5=0与圆x2+y2+2x-4y-4=0的交点为A,B,(1)求线段AB的垂直平分线的方程;
(2)求线段AB的长.
分析 (1)线段AB的垂直平分线的方程,即两圆的圆心的连线MN,用两点式求得MN的方程.
(2)先求得公共弦AB的方程为 4x+4y-1=0,由于圆N的半径为3,求得点N到AB的距离为d,再利用弦长公式求得线段AB的长.
解答 解:(1)圆M:x2+y2-2x-5=0,即 (x-1)2+y2=6,表示以M(1,0)为圆心、半径等于$\sqrt{6}$的圆.
圆N:x2+y2+2x-4y-4=0,即(x+1)2+(y-2)2=9,表示以N(-1,2)为圆心、半径等于3的圆.
由于两圆的交点为A,B,故AB为公共弦,故AB的垂直平分线即两圆的圆心的连线MN,
故线段AB的垂直平分线的方程为 $\frac{y-0}{2-0}$=$\frac{x-1}{-1-1}$,即 x+y-1=0.
(2)把两圆的方程相减,可得公共弦AB的方程为 4x+4y-1=0,
圆N的半径为3,点N(-1,2)到AB的距离为d=$\frac{|-4+8-1|}{\sqrt{16+16}}$=$\frac{3\sqrt{2}}{8}$,故弦长AB=2$\sqrt{{r}^{2}{-d}^{2}}$=2$\sqrt{9-\frac{18}{64}}$=$\frac{3\sqrt{62}}{4}$.
点评 本题主要考查圆的标准方程,圆和圆的位置关系,点到直线的距离公式、弦长公式的应用,属于中档题.

练习册系列答案
相关题目
17.已知函数f(x)=2sinxsin(x+$\frac{π}{3}$+φ)是奇函数,其中φ∈(0,π),则函数g(x)=cos(2x-φ)的图象( )
| A. | 关于点($\frac{π}{12}$,0)对称 | |
| B. | 可由函数f(x)的图象向右平移$\frac{π}{3}$个单位得到 | |
| C. | 可由函数f(x)的图象向左平移$\frac{π}{6}$个单位得到 | |
| D. | 可由函数f(x)的图象向左平移$\frac{π}{12}$个单位得到 |
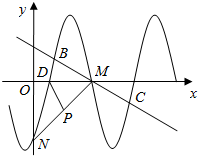 函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示.其中L,M,N分别是函数f(x)的图象与坐标轴的交点.且LM=3OL,∠NM0=45°,线段MN的中点P的坐际为(2,一2).
函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示.其中L,M,N分别是函数f(x)的图象与坐标轴的交点.且LM=3OL,∠NM0=45°,线段MN的中点P的坐际为(2,一2).